author: luwei date: 2025-10-5 version: v0.6.6 revise time:2025-10-16
Description:根据我的纸质笔记通过Qwen-3 MAX转换得到的电子版数学笔记。记录零散,非按章节整理。
考研数二—高数笔记
考研数二—高数笔记1.
1.
解法(分部积分 + 凑微分):
首先,利用凑微分:
原式可改写为:
应用分部积分公式
最终结果:
2.
注意:绝对值勿漏!
3. 不等式:
来源:2026版 张宇《1000题》第6章第6题;25基础30讲P53
4. 立方和与立方差公式
立方和公式:
立方差公式:
5. 常用积分与恒等式
重要恒等式:
6. 二倍角公式
基本形式:
推导形式:
7. 积分公式:
8. 关于
方法: 分子分母同除以
9. 三角代换(用于根号内含平方项)
10. 三角恒等式推导
由基本恒等式
两边同除以
两边同除以
11. 特殊三角函数积分
12. 万能公式(Weierstrass substitution)
令
由此可得:
正弦:
余弦:
正切:
用途: 将任意关于
和 的有理函数积分转化为关于 的有理函数积分。
13. 形如
解法:
设分子为分母及其导数的线性组合:
其中:
代入并比较系数,解出常数
则原积分为:
14.
标准结果:
也可写作
,两者等价。
15. 积化和差公式
16. 辅助角公式
对于形如
其中:
也可写成
,其中 。
17. 反常积分敛散性“万能公式”
考虑积分:
其敛散性需分别讨论在
当
若
若
否则发散。
当
若
若
否则发散。
结论: 整个积分收敛当且仅当两端均收敛。
18. 关于
该积分是收敛的。
虽然当
补充: 实际上,
(可通过换元 证明)。
19. 高斯积分与伽马函数
高斯积分:
Γ函数 (Gamma Function)
定义:
注:通过变量代换
递推公式:
即:
(当 为非负整数时) Tips: 详见《25基础30讲》P179。
20. 积分绝对值不等式
对于
说明: 这是积分基本性质之一,源于绝对值三角不等式。
21. 柯西-施瓦茨不等式(积分形式)
来源:凯积分不等式专题 P11
对于区间
更标准的形式(平方积分):
或写成:
22. 特殊积分恒等式
推导提示: 利用区间对称性(令
),再相加即可推得。
23. 半圆面积公式
几何意义: 此积分表示半径为
的上半圆在第一象限部分的面积,即四分之一圆的面积。
24. 伽马函数与阶乘的关系
说明: 这是伽马函数
在正整数上的特例。
25. 周期函数的积分性质
设
在一个完整周期内积分值相同:
在
26. 关于
图示:
从
从
结论: 一个完整周期内
的积分为 。
27. 利用二重积分计算平面图形的面积
设平面区域
核心思想: 将面积微元
转换为极坐标下的扇形面积微元 。
28. 利用二重积分计算旋转体体积
设平面区域
其中,
原理: 帕普斯定理(Pappus's Centroid Theorem)的积分形式。
29. 函数
讨论不同
①
②
③
备注: 当
时,图形趋近于单位正方形;当 时,图形趋近于坐标轴。
30. 利用二重积分定义求极限
考虑极限:
这实际上是函数
说明: 当
时, , ,划分趋于无穷细。
31. 利用定积分定义求极限(一维情况)
考虑极限:
这是函数
核心思想: 将离散求和转化为连续积分,是考研数学中常见的极限计算方法。
32. 矩形区域上的二重积分可分离性
设积分区域
用途: 常用于利用二重积分证明积分不等式,通常需结合轮换对称性或变量代换。
33. 二重积分的轮换对称性
如果积分区域
函数值交换:
坐标变量交换:
函数平均值:
核心思想: 利用对称性简化计算或证明等式/不等式。
34. “点火公式”(Wallis 公式 / 三角函数幂次积分)
① 定义与基本关系:
令
若
若
注意:偶数情形的最后一个分数是
,不是 。
② 扩展到
③ 扩展到
记忆口诀: “点火公式”中,偶数次幂结果含
,奇数次幂结果不含;区间扩大一倍,积分值相应加倍(偶函数)或为零(奇函数)。
35. 形如
解法推荐:分子有理化
原式:
分子分母同乘
拆分为两项:
分别求解:
第一项是反正弦函数:
第二项用凑微分:
最终结果:
替代方法: 也可令
,但过程较繁琐,推荐使用上述“分子有理化”法。
36.
展开式:
通式:
其中,组合数
性质:
共有
项。 第
项为 。
37. 一阶微分方程求解
① 可分离变量型微分方程
形式:
解法:
将变量分离:
两边同时积分:
② 齐次型微分方程
形式:
解法:
令
代入原方程:
整理为可分离变量形式:
两边积分即可求解。
③ 一阶线性微分方程
形式:
形如
通解公式:
Tips: 推导过程详见《25张宇基础30讲》P269。
38. 伯努利方程 (仅数一)
Tips: 数二考生亦可通过提示“换元”解题。
形式:
解法:
变形: 方程两边同除以
换元: 令
代入: 将上式代入变形后的方程:
求解: 此时得到一个关于
39. 二阶可降阶微分方程
(1)
解法:
令
这是一个关于
解得其通解为
由于
再对
(2)
解法:
令
这是一个关于
解得其通解为
由于
分离变量得:
两边积分得:
即得原方程的通解。
(3)
此类型既不显含
Tips: 通过换元法将其化为一阶方程求解。
40. 二阶常系数齐次线性微分方程
标准形式:
理论基础:
若
求解步骤:
写出特征方程:
求特征根:
根据特征根的不同情况,写出通解:
① 两个不相等的实根 (
② 两个相等的实根 (
③ 一对共轭复根 (
41. 二阶常系数非齐次线性微分方程
标准形式:
其中
通解结构
若
核心思想: 非齐次方程的通解 = 齐次方程的通解 + 非齐次方程的一个特解。
解的叠加性
若
若
特解的设定方法(待定系数法)
① 当
其中
特解形式:
提示: “
照抄”,只需确定 值。
② 当
其中
特解形式:
提示: “
照抄”,只需确定 值。
示例
例1:求解
求齐次通解: 特征方程:
设特解:
代入原方程求系数:
写出通解:
例2:求解
求齐次通解: 同上,
设特解:
注意: 此处的
是为了消除与齐次解的重复项。
42.
对于形如
① 若
② 若
③ 若
核心思想: 每一个特征根对应一组基本解,所有基本解的线性组合即为通解。
43. 欧拉方程 (仅数一)
Tips: 数二考生亦可通过提示“换元”解题。
标准形式:
解法:
当
一阶导数:
二阶导数:
代入原方程,化简得:
此为常系数线性微分方程,可按常规方法求解。
最后,用
当
44. 关于
若要求
特征根
且此时必有
说明: 这是保证解在无穷远处衰减到零的必要条件,从而使得积分收敛。
45. 求解一阶线性微分方程的通解时,若原式不满足常见形式
当原方程无法直接写成
其中
这样,原方程就变成了关于
46. 使用变限积分表达的一阶线性微分方程通解
一阶线性微分方程
该公式亦可写成变限积分形式:
Tips: 在使用变限积分求导时,被积函数中不能含有求导变量(即积分上限或下限中的变量)。
参考: 见《26 张宇 1000题》第15章第10题。
47. 拉格朗日乘数法 (求极值)
问题: 求目标函数
解法步骤:
构造辅助函数(拉格朗日函数):
注: 辅助函数中的自变量个数 = 目标函数自变量个数 + 约束条件个数。
令所有偏导数为零:
解方程组: 解得备选点
确定最值: 取其中的最大值
Tips: 对于简单函数,可考虑直接将约束条件代入目标函数消元;对于复杂函数,则需使用拉格朗日乘数法。
48. 无条件极值 (二元函数)
设函数
步骤:
求驻点: 解方程组
二阶充分条件: 记
并计算判别式
若
若
若
补充说明: 对于一般函数,若在
处的极限 与函数值 不相等,或极限不存在,该点不是极值点。通常在考研数学中,判别法失效的情况下,极值大概率不存在,但需要证明。
49. 全微分形式不变性
设
则
核心性质:
无论
解释: 这是因为多元函数微分遵循链式求导法则,求导后新函数与原函数具有完全相同的复合结构。
50. 隐函数求导 (公式法)
① 二元隐函数
若方程
则在该点附近可确定一个单值函数
② 三元隐函数
若方程
则在该点附近可确定一个单值函数
51. 一元函数与多元函数的性质关系图
下图为一元函数和多元函数中“可微”、“连续”、“极限存在”、“可导/偏导存在”之间的逻辑关系总结:

关键点:
对于一元函数,“可微”与“可导”是等价的。
对于多元函数,“可微”蕴含“连续”和“偏导存在”,但“偏导存在”不能推出“可微”,“连续”也不能推出“可微”。
52. 可微的判别步骤 (以二元函数为例)
判断函数
计算全增量:
写出线性增量:
其中
作极限判断:
若该极限等于
Tips: 一元函数可微的判别方法:
计算
。 线性增量为
。 判断极限:
若成立,则
在 处可微。
53.微分与导数的关系
1. 微分的定义
在点
解释:
这个公式表明:微分 = 导数 × 自变量微分。
2. 函数增量与微分的关系
函数在
解释:
这个等式说明:函数的真实增量 = 线性近似(微分)+ 高阶无穷小误差。
3. 导数的极限定义与微分的关系推导
通过极限过程,可以从增量比推导出导数:
详细推导说明:
将
由于
当
第一项
第二项
因此:
这正是导数的定义!它从“微分近似”的角度重新验证了导数的极限本质。
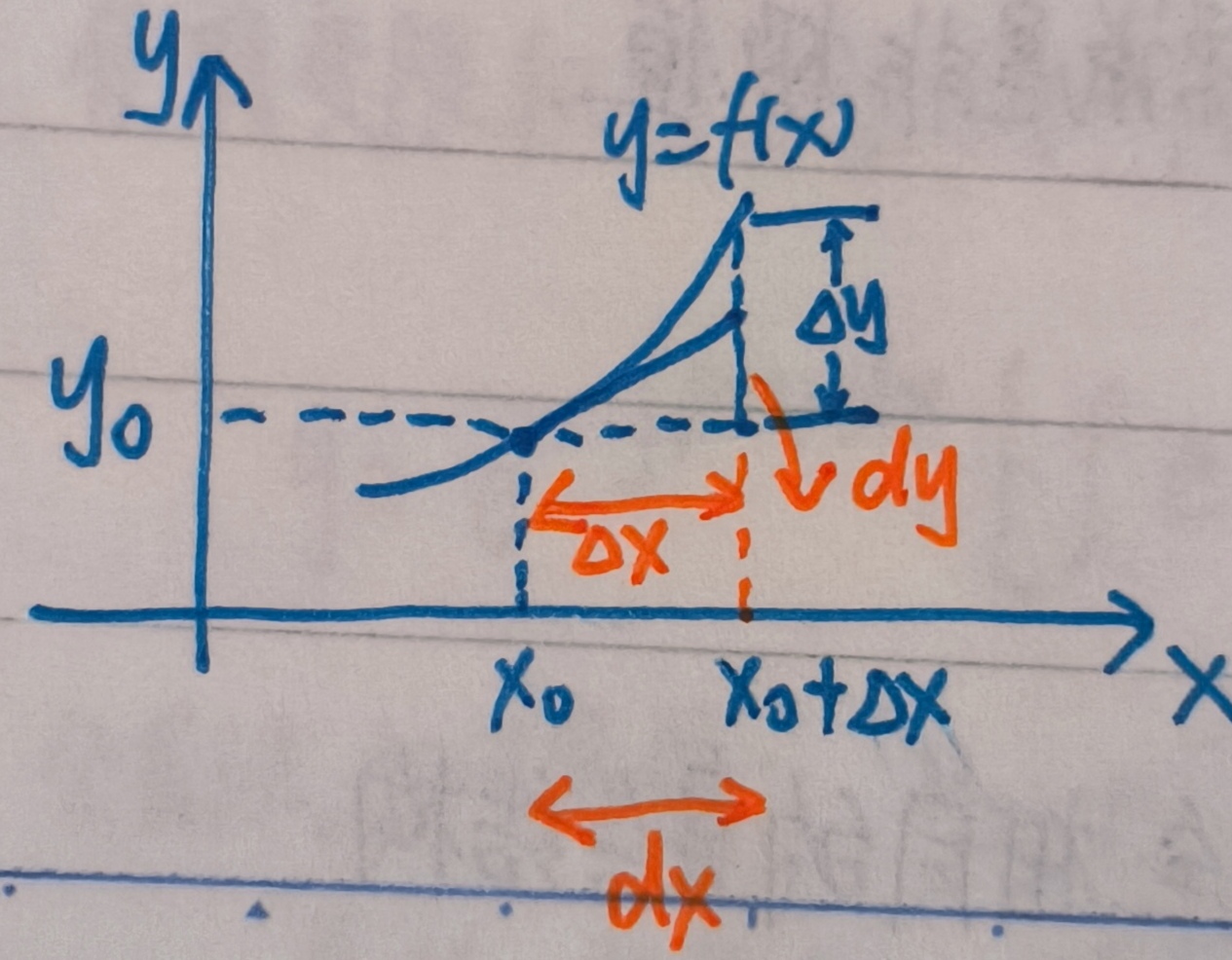
导数
是函数在某点的变化率,而微分 是利用这个变化率对函数增量进行线性近似的结果。
54. 均值不等式 (调和平均 ≤ 几何平均 ≤ 算术平均 ≤ 平方平均)
对于
等号成立条件: 当且仅当
时取等号。
Tips: 相关题目见《张宇1000题》第13章第21题;《凯哥讲义3》P14。
55. 柯西不等式 (Cauchy-Schwarz Inequality)
对于两组实数
等号成立条件: 当且仅当两组数成比例,即存在常数
使得 ( ) 时取等号。 注意: 笔记中“均为非负实数”的限定并非必要,柯西不等式对任意实数均成立。
56. 积分的物理应用
① 位移大小:
若速度函数为
② 总路程:
总路程是速度的绝对值积分:
③ 做功:
若力
④ 从容器中抽出液体所做的功:
设液体密度为
其中,
⑤ 静水压力:
作用在竖直平板上的静水压力,若平板在深度范围
⑥ 细杆质心:
若细杆在区间
57. 关于
这类问题通常与微分中值定理相关,核心思想是将函数值之差转化为导数或积分形式。
① 牛顿-莱布尼茨公式 (微积分基本定理)
若函数
要求:
在 上连续,且 存在(或至少可积)。
② 拉格朗日中值定理
若函数
Tips: 相关题目见《张宇1000题》第11章第9题。
58. 复合函数的单调性
复合函数
内外层函数单调性相同:复合函数为增函数。
内外层函数单调性相反:复合函数为减函数。
记忆口诀: “同增异减”。
59. 变限积分
基本性质:
若
推广形式(莱布尼茨公式):
若
Tips:
只要
在积分区间上可积,变限积分函数 一定连续。 对变限积分求导时,被积函数中不能含有求导变量
(即积分上下限中的变量)。
60. 关于
函数
61. 平面图形面积
① 直角坐标系下:
由两条曲线
② 极坐标系下:
由两条极径曲线
62. 旋转体体积
① 绕
由曲线
② 绕
由曲线
③ 绕任意直线
由曲线
Tips: 记忆口诀:“面积 × 走过的路”。即体积等于截面面积乘以质心走过的距离(帕普斯定理)。
63. 形心坐标公式
设平面区域
Tips:
当积分区域
为圆形时,由于对称性,形心 已知。 此时,有
, ,可以简化二重积分运算。
64. 平面曲线的弧长公式
① 显函数形式:
若曲线方程为
② 参数方程形式:
若曲线方程为
③ 极坐标形式:
若曲线方程为
65.曲率及曲率半径公式
设
曲率半径的计算公式
注:弯曲程度越大,曲率越大,曲率圆的半径越小。
66.
对于任意实数
67. 反三角函数的复合关系与图像
① 复合关系:
但
② 函数
该函数是一个周期为
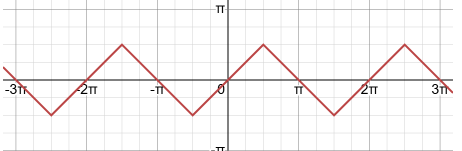
图像特征: 在每个长度为
的区间内,图像是斜率为 1 或 -1 的线段,整体呈“之”字形。
68. 等差数列与等比数列
① 等差数列:
通项公式:
前
② 等比数列:
通项公式:
前
特殊情况:当
求和公式:
69. 椭圆方程
① 横椭圆(长轴在
标准方程:
参数方程:
② 纵椭圆(长轴在
标准方程:
参数方程:
Tips: “大者为
”,即 总是半长轴,决定椭圆的“定轴向”。
③ 椭圆面积与焦距:
面积:
焦距:
70. 已知
若题目给出导函数
71. 双曲正弦函数
这是一个重要的反双曲函数,其性质如下:
奇偶性:
导数:
渐近行为: 当
72. 导数的定义表达式
设函数
增量形式:
差商形式:
导函数定义:
Tips:
对称导数:
存在,不能保证 存在(仅当 在 处连续时等价) 导数
存在 左右导数存在且相等。
73. 绝对收敛蕴含收敛
若反常积分
结论: 绝对收敛 ⇒ 收敛。
74. 渐近线
① 垂直渐近线:
若
则直线
② 水平渐近线:
若极限
③ 斜渐近线:
若极限
求解步骤:
先求
。 再求
。 得到斜渐近线方程
。
75. 高阶无穷小的运算
对于任意实数
含义: 一个无穷小量乘以另一个更高阶的无穷小量,结果仍是更高阶的无穷小量。
76. 可积的充分条件
在闭区间
连续函数: 若
单调函数: 若
有界且仅有有限个间断点: 若
重要提示:
“
可积”意味着其原函数存在,但反之不成立。即“在积分区域上存在原函数”是“可积”的必要条件,而非充分条件。 因此,“
可积 在积分区域上存在原函数”的说法是错误的。
77. 表格法求解积分 (分部积分法)
表格法是处理形如
方法步骤:
列表: 将被积函数中的一个部分(通常是多项式)设为
求导与积分: 对
相乘与符号: 从左上角开始,将
最后项: 最后一项是

示例:求
计算:
78. 关于
这类积分可以通过构造一个二阶线性方程组来求解,或者直接使用公式:
推导思路: 设
, ,通过两次分部积分,可以得到关于 和 的方程组,联立求解即可。
79. 旋转曲面的面积 (侧面积)
① 显函数形式
② 参数方程形式
③ 极坐标形式
核心思想: 侧面积 = 曲线长度 × 旋转半径(平均值)。
80. 放缩常用的不等式
本节汇总了一系列在证明题和求极限中常用的放缩技巧。
① 平均值放缩
对于任意实数
当所有
② 绝对值三角不等式
推广到
③ 均值不等式链
对于非负实数
二元情况:
三元情况:
④ 幂函数单调性
设
当
当
⑤ 分式不等式
若
⑥ 三角函数不等式
在
对于
在
在
⑦ 积分的绝对值不等式
解释: “积分的代数和”的绝对值 ≤ “各部分绝对值之和”。
⑧ 反三角函数不等式
应用: 可用于证明数列
的单调性,例如当 时, ,故 单调减少。
⑨ 指数不等式
⑩ 对数不等式
⑪ 对数函数不等式
对于
Tips: 上述不等式均可通过拉格朗日中值定理证明。
⑫ 最值定理
利用闭区间上连续函数必有最大值和最小值的性质进行放缩。
⑬ 压缩映射原理
i. 数列收敛判定:
对数列
则数列
证明:
故 ,即 收敛于 。
ii. 迭代数列收敛判定:
对数列
证明: 由拉格朗日中值定理,存在
介于 与 之间,使得: 由 i 知, 收敛于 。
81. 反常积分计算
反常积分的计算需特别注意其收敛性,通常按以下步骤进行:
存在瑕点,拆区间: 若积分区间内或端点处存在瑕点(被积函数无界),需将积分区间在瑕点处拆开。
拆成多积分(分部),考虑每一项敛散性: 将原积分拆分为多个定积分或反常积分,分别判断其敛散性。若其中任意一项发散,则整个积分发散。
利用分部积分法时,有:
对于无穷区间
可将其拆为
对于
对于
82. 区间再现公式
设函数
基本形式:
推论:
三角函数应用:
用途: 简化对称区间的积分计算。
83.
(1)
此时
注 (1) 若
为连续的奇函数,则 也是偶函数,故 的全体原函数均为偶函数。 (2) 只需要被积函数可积,即可有变限积分的相关性质,只有被积函数连续时,才能谈原函数的相关性质,以下同。
(2)
此时
注:若
为连续的偶函数,则 的全体原函数中,只有 是奇函数。
(3)
注:
亦是以 为周期的周期函数 。 因为, 为常数, 为周期函数。
84. 高阶导数(莱布尼兹公式)
莱布尼兹公式用于求两个函数乘积的高阶导数。
加法形式:
乘法形式:
或者写成求和形式:
其中,组合数
记忆方法: 系数遵循杨辉三角(帕斯卡三角):
Tips: 一般高阶导数题目建议逐级求导,寻找规律,而非直接套用公式。
85. 凹凸性判别和拐点
① 凹凸性判别:
设函数
若
若
记忆口诀: “二阶导正,图形上凹;二阶导负,图形下凸”。
② 拐点判别:
拐点是曲线凹凸性改变的点。若
必要条件:
充分条件: 在
高阶导数法: 若
核心思想: 拐点是“曲率”发生改变的点,即二阶导数变号的点。
86. 极值点的判定
必要条件:
若函数
注意: 此为必要条件,非充分条件。满足
的点称为驻点,驻点不一定是极值点。
Tips: 驻点一定是可导点,称
, 为驻点。但驻点不一定为极值点。
判别极值的充分条件:
第一充分条件(利用一阶导数符号变化):
若
左正右负
左负右正
第二充分条件(利用二阶导数):
若
高阶导数法:
若
当
当
87. 极值点与拐点的结论
① 基本关系:
不可导点可以同时是拐点和极值点。
可导点不能同时是拐点和极值点。(因为极值点要求一阶导数为零或不存在,拐点要求二阶导数变号,两者在可导点处的条件冲突。)
② 特殊函数形式:
对于形如
当
当
③ 一般多项式函数:
对于形如
记:
则:
极值点个数为
拐点个数为
另一种解法:通过求导找零点个数
示例1: (2001年真题)
函数
分析: 函数有重根
求导: 对
结论: 该函数有 2个拐点。
示例2: (2011年真题)
函数
分析: 通过求导并分析各阶导数的零点重数来判断。
结论: 该函数有 6个驻点,5个极值点,6个拐点。

判断驻点、极值点、拐点个数的方法总结:
驻点个数: 等于
极值点个数: 等于
拐点个数: 等于
核心思想: 通过分析导数的零点及其重数来判断函数图像的关键特征点。
88. 反常积分敛散性
① 比较判别法
设
若
若
② 极限比较判别法
设
当
若
当
若
当
推论:
当
时,若 和 为同阶无穷小,则两个积分同敛散。 当
时,若 和 为同阶无穷大,则 和 同敛散。
89.P积分的敛散性
① 无穷区间上的P积分:
对于
Tips: 对于
,无论 取多少都发散(因为其在 和 两端均可能发散)。
② 瑕积分上的P积分:
对于
90.广义P积分敛散性
形如
通过换元(如令
① 对于
② 对于
核心思想: 广义P积分的敛散性判断与标准P积分类似,关键在于看对数项的幂次
。
91.
该恒等式为:
注意: 此恒等式在
处无定义,因为 无意义。
92. 中值定理
① 罗尔定理 (Rolle's Theorem)
设函数
② 拉格朗日中值定理 (Lagrange's Mean Value Theorem)
设函数
③ 积分中值定理 (Integral Mean Value Theorem)
设函数
④ 介值定理 (Intermediate Value Theorem)
闭区间上的连续函数,一定可以取到介于其最大值和最小值之间的任意值。
⑤ 柯西中值定理 (Cauchy's Mean Value Theorem)
设函数
Tips: 在以上所有中值定理中,只有介值定理中的
落在闭区间 上(积分中值定理也是);其余定理中的 均落在开区间 内。
93. 积分因子法构造辅助函数
“常用来解中值定理证明题”
对于形如
原理:
对
因此,若
Tips: 在表达式
上乘以积分因子 后,恰好可以凑成一个函数的导数形式。
特殊情况: 若
是一个抽象函数,则需要将公式修改为:
94. 泰勒定理 (出现高阶导数时)
泰勒定理是处理涉及高阶导数问题的核心工具。
1. 带佩亚诺余项的泰勒展开 (用于计算极限)
若函数
特点: 仅需知道
在 点的各阶导数值,即可写出其局部近似多项式。余项 表示当 时,余项比 更高阶无穷小。 用途: 主要用于求极限或分析函数在某点附近的性态。
2. 带拉格朗日余项的泰勒展开 (用于证明中值定理问题)
若函数
其中
特点: 余项是一个具体的表达式,包含一个未知点
的 阶导数。 用途: 主要用于证明题,特别是需要利用中值定理思想的问题。
Tips: 选择导数信息多的点作为
,而只知道函数值、不知道导数信息的点作为 。
3. 当
将上述泰勒公式中的
带拉格朗日余项:
带佩亚诺余项:
4. 几个重要函数的麦克劳林展开式
以下是几个常用初等函数在
① 指数函数:
② 正弦函数:
③ 余弦函数:
④ 几何级数:
⑤ 有理函数:
⑥ 对数函数:
⑦ 幂函数:
核心价值: 这些展开式是进行极限计算、函数逼近和证明题的有力工具。
95. 零点定理 (Intermediate Value Theorem for Roots)
若函数
核心思想: 连续函数在区间两端异号,则必穿过零点。
96. 罗尔定理推论
若函数
解释: 这是罗尔定理的推广。每求一次导数,方程的根的个数最多减少一个。因此,如果第
阶导数有 个根,那么原函数最多有 个根。 记忆口诀: “阶数换根的个数”。
97. 泰勒公式 (重要函数的展开式)
以下是几个重要函数在
98. 常用等价无穷小和重要极限公式
当
等价无穷小:
高阶无穷小(差值):
Tips: 这些高阶无穷小关系常用于计算极限中的“差值”问题。
99. 幂指函数的处理方法
对于形如
100. 对数函数的等价关系
当
Tips: 此关系可由
( ) 推导得到,令 即可。常用于计算 型极限。
101. 计算
对于形如
用途: 主要用于计算
型极限。
102.
若函数
Tips: 详见《25基础30讲》P65。
103. 重要极限公式
Tips: 求极限时,
,抓 的最高次项; ,抓 的最低次项。
104.积分基本公式汇总
本节汇总了最常用的基本积分公式,是求解不定积分的基础。
① 幂函数积分
特例:
② 对数函数积分
③ 指数函数积分
提示:
,因此积分时需除以 。
④ 三角函数积分
基本三角函数:
正切与余切:
正割与余割:
平方三角函数:
乘积形式:
提示:
; 。
⑤ 反三角函数相关积分
⑥ 反三角函数相关积分
⑦ 根式积分
⑧ 分式积分
⑨ 根式积分
⑩ 三角函数平方积分
正弦与余弦平方:
正切与余切平方:
105.基本求导公式
本节汇总了最常用的基本求导公式,是求解导数的基础。
幂函数与指数函数:
对数函数:
三角函数:
反三角函数:
特殊函数与商法则:
106.三角诱导公式
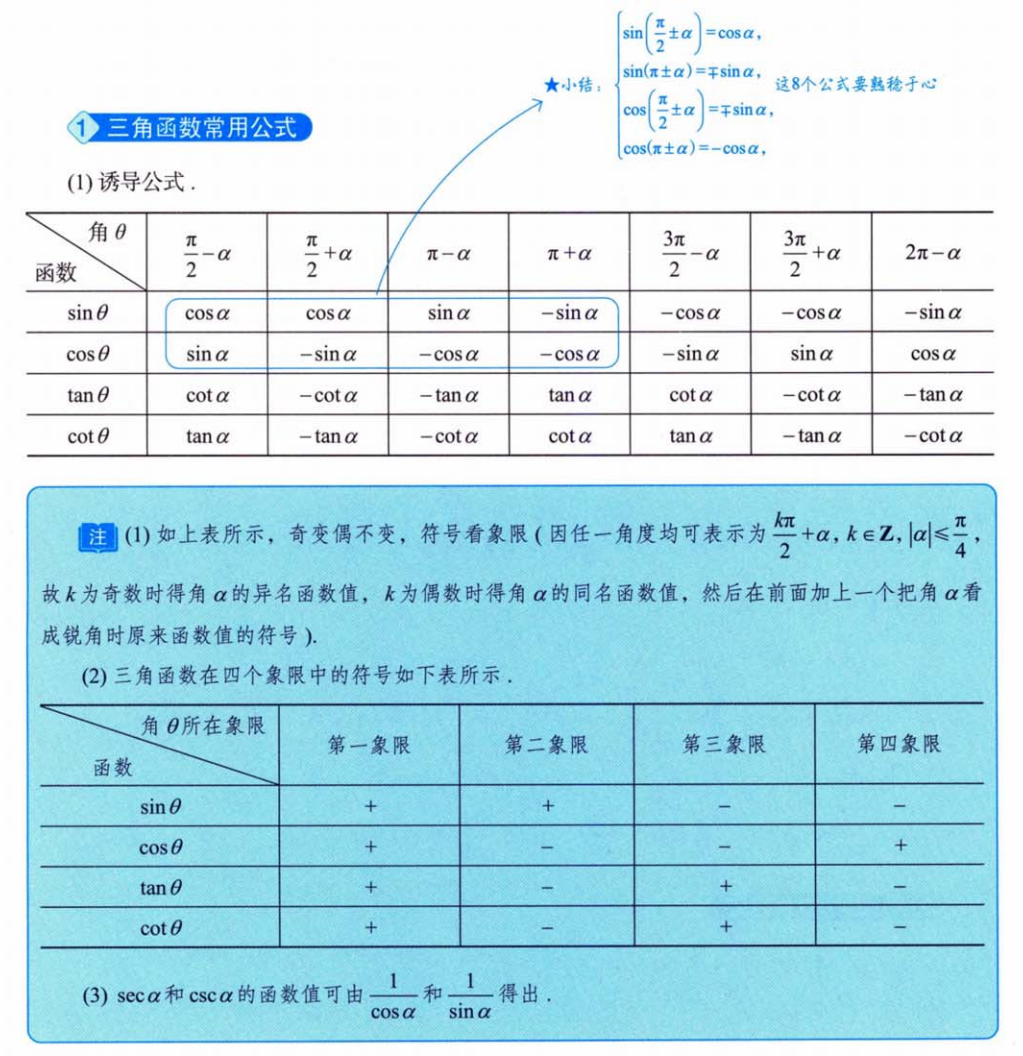
107.三角函数图像
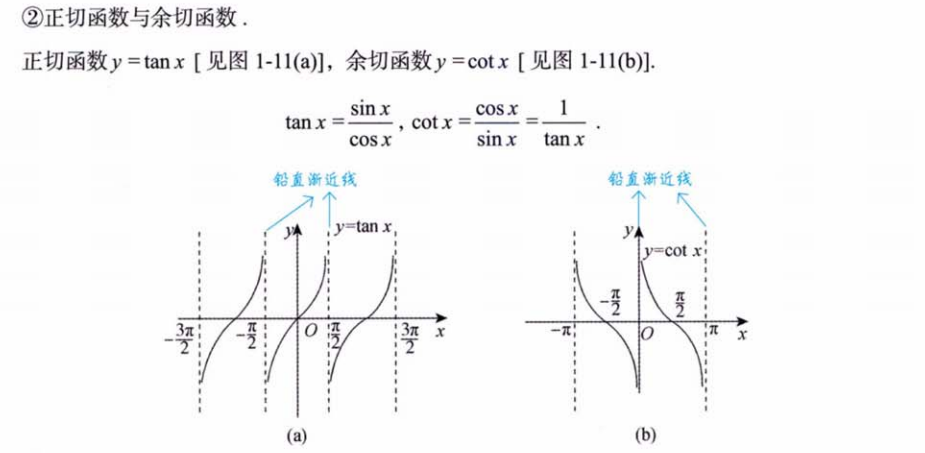
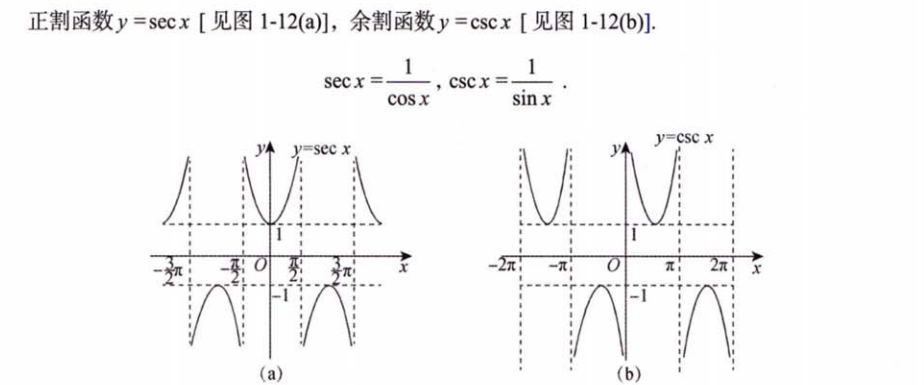
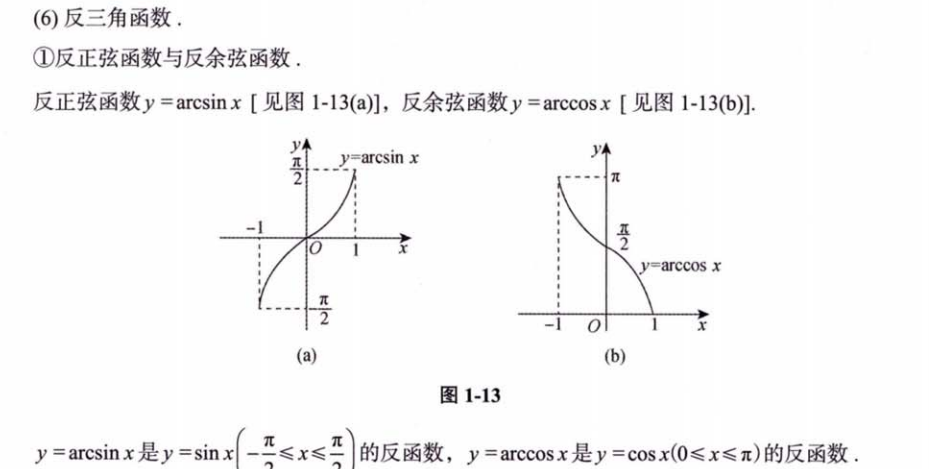

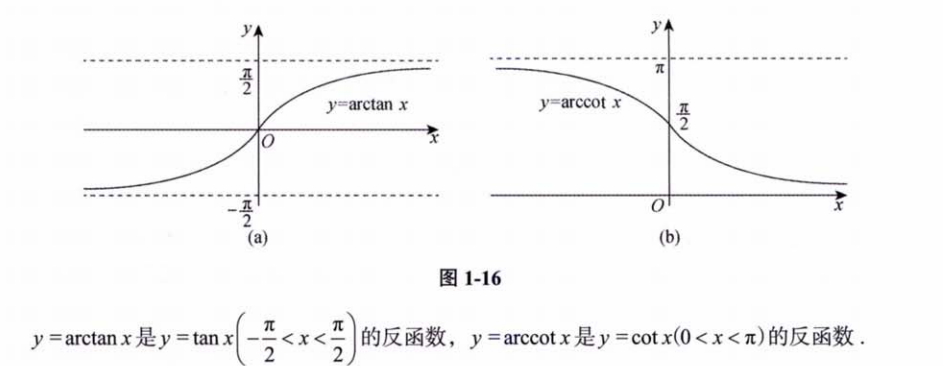
108.常见的平面图形
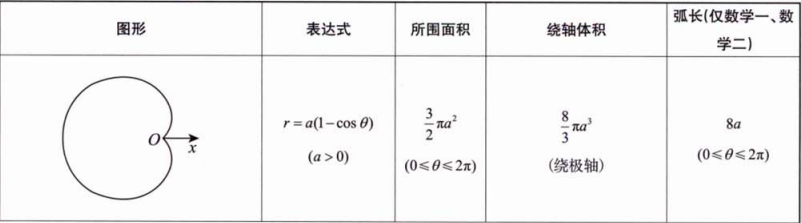
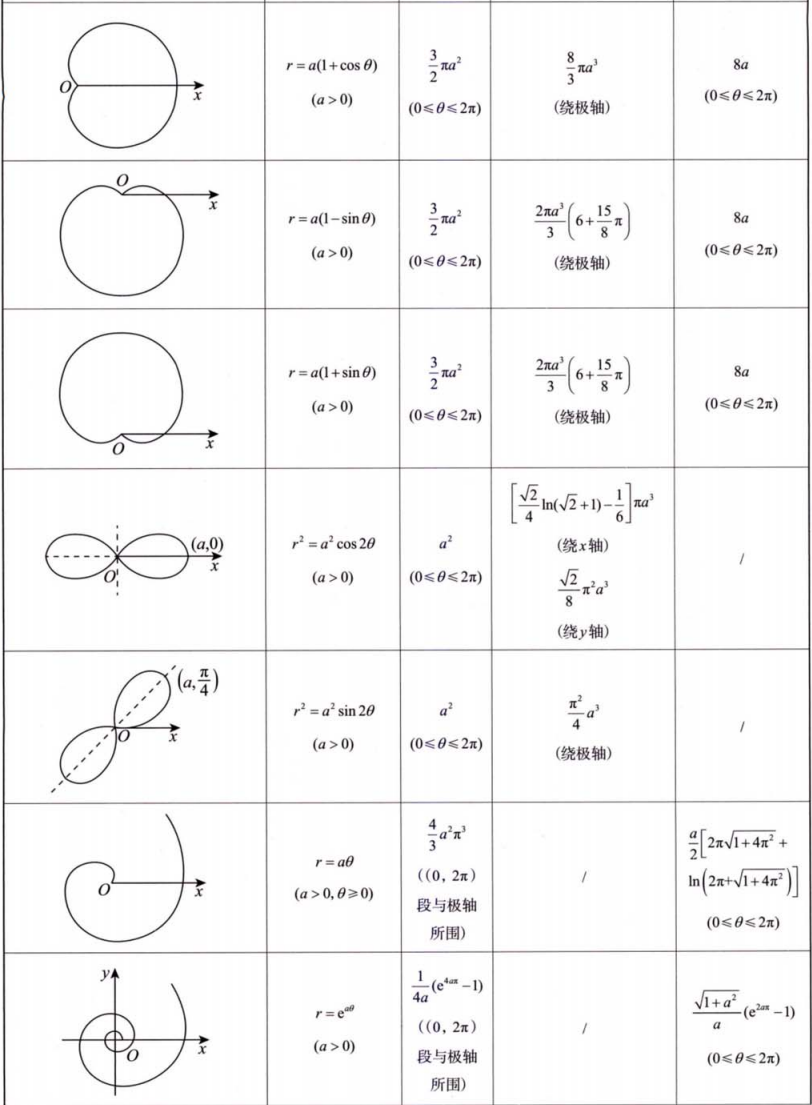
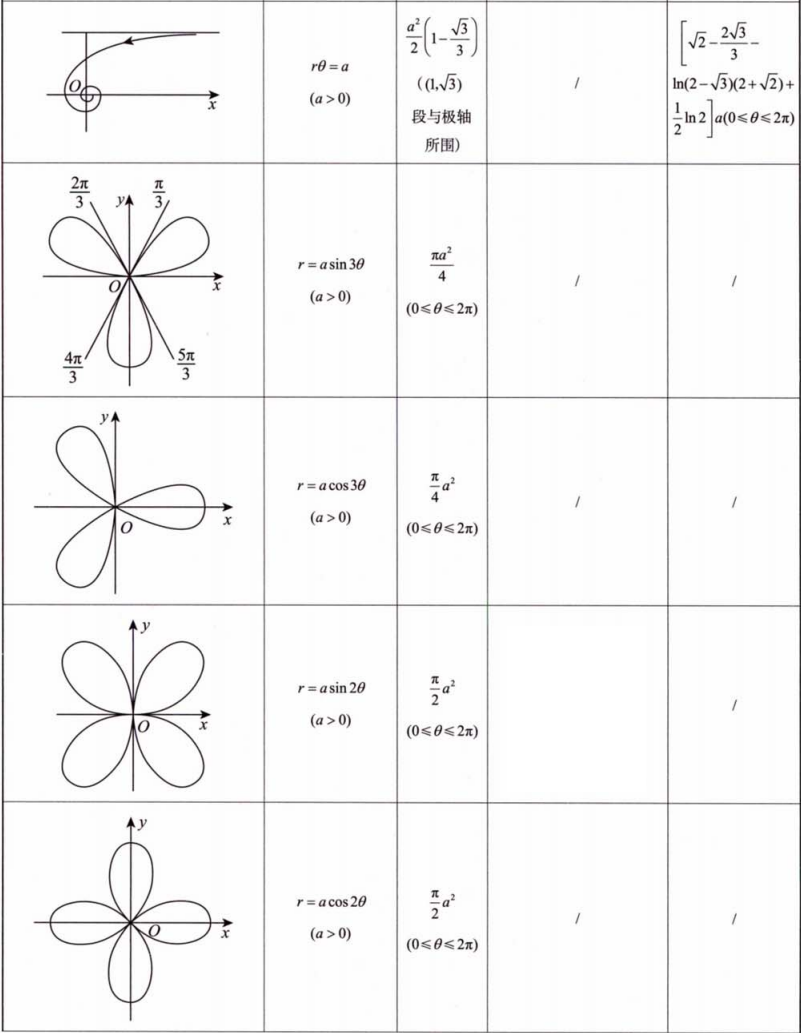
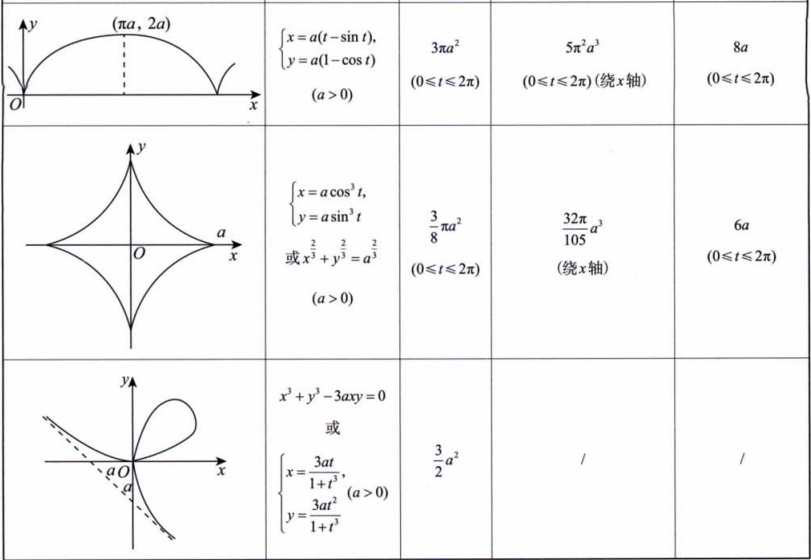
备注: 笔记中部分公式可能因手写识别或排版存在小误差,以上已根据标准数学表达式进行校正。建议在使用时结合教材或权威资料核对。
