author: luwei date: 2025-10-17 version: v0.6.6 revise time:2025-10-24

Description：根据我的纸质笔记通过Qwen-3 MAX转换得到的电子版数学笔记。记录零散，线代按章节整理。

🏠 回到主页

考研数二—线代笔记

一、行列式

1. $f(x)=x^n+a_{n-1}{x}^{n-1}+\cdots +a_{1}x+a_0$$f(x) = x^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0$

若 $f(x)=x^n+a_{n-1}{x}^{n-1}+\cdots +a_{1}x+a_0$$f(x) = x^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0$ 为 n 次函数，则 $f(x)=0$$f(x)=0$ 的 n 个实根分别记为 $x_1,x_2,\cdots ,x_n$$x_1, x_2, \cdots, x_n$，则必有 $\sum _{i=1}^n{x}_i=-a_{n-1}$$\sum_{i=1}^{n} x_i = -a_{n-1}$

例: $a,b,c$$a, b, c$ 是 $x^3-2x+4=0$$x^3 - 2x + 4 = 0$ 的三个根，则 $x^3-0x^2-2x+4=0$$x^3 - 0x^2 - 2x + 4 = 0$，$a+b+c=-0=0$$a+b+c = -0 = 0$

2. 求行列式（含 x）展开式中的常数项，直接令行列式中 $x=0$$x=0$，直接求值即得。

3. 行列式性质

① $|A|=|A^T|$$|A| = |A^T|$，行列互换，其值不变

② 某行(列)元素全为 0，行列式为 0

③ 单行可提性，可将公因子 $k(k\ne 0)$$k (k \neq 0)$ 提出

④ 单行(列)可拆性，

注意逆用

⑤ 两行(列)换号，行列式变号

⑥ 两行成比例，行列式值为 0

⑦ 将某行(列)的 k 倍加到另一行(列)，行列式不变

4. 余子式、代数余子式

余子式: 去掉 $a_{ij}$$a_{ij}$ 所在行列后拼起来的 (n-1) 阶行列式，记作 $M_{ij}$$M_{ij}$

代数余子式: 记作 $A_{ij}=(-1{)}^{i+j}{M}_{ij}$$A_{ij} = (-1)^{i+j} M_{ij}$

行列式展开公式: 行列式等于行列式的某行(列)元素分别相乘其相应代数余子式求和 但行列式某行(列)元素分别乘以另一行(列)元素的代数余子式后再求和结果为 0。

例如求解:

将 $A_{3j}$$A_{3j}$ 对应系数，替换原 $|A|$$|A|$ 相应值，再求行列式值。

5. 主对角行列式

主对角行列式的值等于主对角线上所有元素的乘积：

副对角行列式

注: 副对角线元素相乘再乘 $(-1{)}^{\frac{n(n-1)}{2}}$$(-1)^{\frac{n(n-1)}{2}}$，以上公式对于三角阵同样成立。

拉普拉斯展开式

设 A 为 m 阶矩阵，B 为 n 阶矩阵，则有：

范德蒙德行列式

关键行: 行列式值为第二行后一项减前一项的所有项的乘积。 （第一行为 $x^0$$x^0$，即常数1；后续行依次为 $x^1,x^2,...,x^{n-1}$$x^1, x^2, ..., x^{n-1}$）

6. 排序和逆序、$n$$n$ 阶行列式的定义

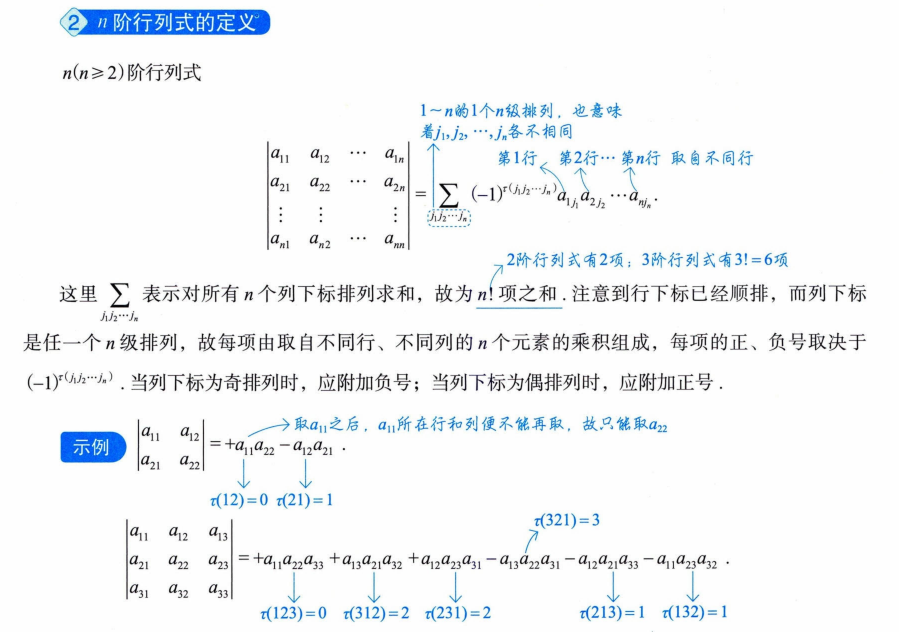
7. 克拉默法则

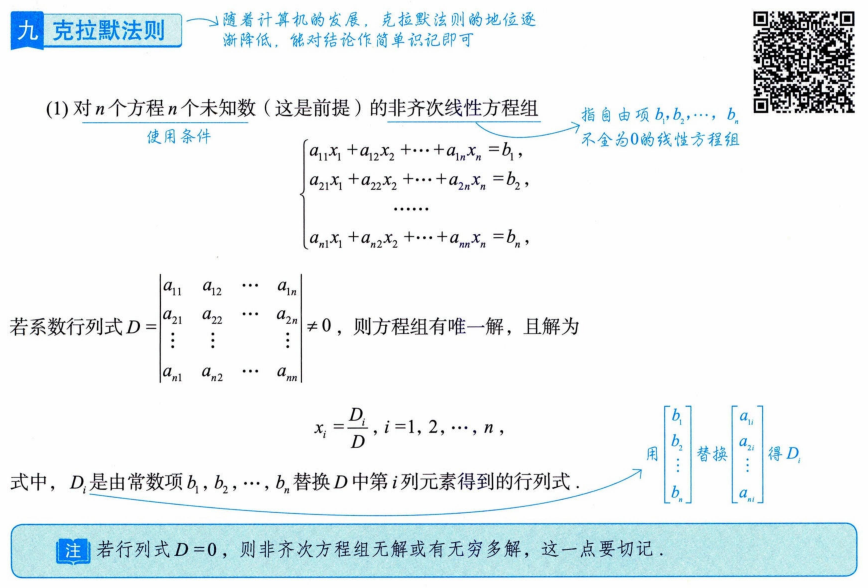
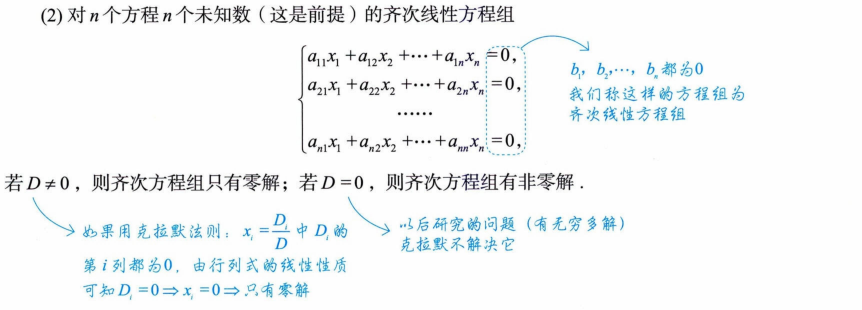
二、矩阵

1. 同型矩阵可相加

$C=A+B=(a_{ij}{)}_{m\times n}+(b_{ij}{)}_{m\times n}=(c_{ij}{)}_{m\times n}$$C = A + B = (a_{ij})_{m \times n} + (b_{ij})_{m \times n} = (c_{ij})_{m \times n}$

即对应元素相加

2. 数乘矩阵

$kA=Ak=(k{a}_{ij}{)}_{m\times n}$$kA = Ak = (ka_{ij})_{m \times n}$

即 A 的每个元素都乘以 k。

3. 运算法则

• 加法交换律: $A+B=B+A$$A + B = B + A$

• 加法结合律: $(A+B)+C=A+(B+C)$$(A + B) + C = A + (B + C)$

• 数乘分配律: $k(A+B)=kA+kB$$k(A + B) = kA + kB$, $(k+l)A=kA+lA$$(k + l)A = kA + lA$

• 数乘结合律: $k(lA)=(kl)A=(lk)A$$k(lA) = (kl)A = (lk)A$

矩阵相乘: $c_{ij}=\sum _{k=1}^s{a}_{ik}{b}_{kj}=a_{i1}{b}_{1j}+a_{i2}{b}_{2j}+\cdots +a_{is}{b}_{sj}(i=1,2,\cdots ,m;j=1,2,\cdots ,n)$$c_{ij} = \sum_{k=1}^{s} a_{ik} b_{kj} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{is}b_{sj} \quad (i=1,2,\cdots,m; j=1,2,\cdots,n)$

转置 (行列互换):

• $(A^T{)}^T=A$$(A^T)^T = A$

• $(kA{)}^T=k{A}^T$$(kA)^T = kA^T$

• $(A+B{)}^T=A^T+B^T$$(A + B)^T = A^T + B^T$

• $(AB{)}^T=B^T\cdot A^T$$(AB)^T = B^T \cdot A^T$

• 结合律: $(AB)C=A(BC)$$(AB)C = A(BC)$

• 分配律: $A(B+C)=AB+AC$$A(B + C) = AB + AC$

• 数乘结合律: $(kA)B=A(kB)=k(AB)$$(kA)B = A(kB) = k(AB)$

注意: 一般地，$AB\ne BA$$AB \neq BA$

行列式相关性质:

• $|kA|=k^n|A|\ne k|A|$$|kA| = k^n |A| \neq k|A|$

一般地, $|A+B|\ne |A|+|B|$$|A + B| \neq |A| + |B|$

• $A\ne O\nRightarrow |A|\ne 0$$A \neq O \not\Rightarrow |A| \neq 0$

• $A\ne B\nRightarrow |A|\ne |B|$$A \neq B \not\Rightarrow |A| \neq |B|$

• $|A^T|=|A|$$|A^T| = |A|$

• 设 A, B 是同阶方阵，则 $|AB|=|A||B|$$|AB| = |A||B|$

对称矩阵与反对称矩阵:

• 对称矩阵: $A^T=A$$A^T = A$

• 反对称矩阵: $A^T=-A$$A^T = -A$

4. 主对角线结论

对于主对角线上元素为 $1,-1,2$$1, -1, 2$ 的矩阵：

其余情况踏踏实实找规律

5. 特殊矩阵的幂

• 对于上三角或下三角矩阵，其幂运算通常保持三角形式。

• 严格三角阵的幂: 例如一个 3 阶严格上三角矩阵的平方：

注：此处 $3=1\times 3$$3 = 1 \times 3$，直观表现为上三角矩阵的各元素往右上角移动，此处示例矩阵的三次方为 0 。

6. 逆矩阵

若存在矩阵 B，使得 $AB=BA=E$$AB = BA = E$，则称 A 可逆，并记 $A^{-1}=B$$A^{-1} = B$，$B^{-1}=A$$B^{-1} = A$。

★ A 可逆的充分必要条件是 $|A|\ne 0$$|A| \neq 0$

$|A|\ne 0⟺A\text{ 可逆}$$|A| \neq 0 \iff A \text{ 可逆}$

若 A, B 为同阶可逆方阵，则有:

• $(A^{-1}{)}^{-1}=A$$(A^{-1})^{-1} = A$

• 若 $k\ne 0$$k \neq 0$，则 $(kA{)}^{-1}=\frac{1}{k}{A}^{-1}$$(kA)^{-1} = \frac{1}{k} A^{-1}$

• $AB$$AB$ 可逆，$(AB{)}^{-1}=B^{-1}{A}^{-1}$$(AB)^{-1} = B^{-1}A^{-1}$ (穿脱原则)

• $A^T$$A^T$ 可逆，$(A^T{)}^{-1}=(A^{-1}{)}^T$$(A^T)^{-1} = (A^{-1})^T$

• $|A^{-1}|=|A{|}^{-1}$$|A^{-1}| = |A|^{-1}$

求解 $A^{-1}$$A^{-1}$ 的方法: ① 定义法: $AB=E$$AB = E$，则 $A^{-1}=B$$A^{-1} = B$ ② 公式法: $A^{-1}=\frac{A^{\ast }}{|A|}$$A^{-1} = \frac{A^*}{|A|}$ (其中 $A^{\ast }$$A^*$ 为 A 的伴随矩阵) ③ 初等行变换法: 将矩阵 $(A,E)$$(A, E)$ 通过初等行变换化为 $(E,A^{-1})$$(E, A^{-1})$

只能作行变换。 或者，将矩阵 $\left(\begin{array}{c}A\\ E\end{array}\right)$$\begin{pmatrix} A \\ E \end{pmatrix}$ 通过初等列变换化为 $\left(\begin{array}{c}E\\ A^{-1}\end{array}\right)$$\begin{pmatrix} E \\ A^{-1} \end{pmatrix}$ 只能作列变换。

7. 伴随矩阵 $A^{\ast }$$A^*$

伴随矩阵 $A^{\ast }$$A^*$ 的定义为：

其中，$A_{ij}=(-1{)}^{i+j}{M}_{ij}$$A_{ij} = (-1)^{i+j} M_{ij}$ 是元素 $a_{ij}$$a_{ij}$ 的代数余子式。

注: A 的第 i 行元素的代数余子式写在 $A^{\ast }$$A^*$ 的第 i 列上。

核心性质:

• $A{A}^{\ast }=A^{\ast }A=|A|\cdot E$$AA^* = A^*A = |A| \cdot E$

• $|A^{\ast }|=|A{|}^{n-1}$$|A^*| = |A|^{n-1}$

• $(A^{\ast }{)}^{\ast }=|A{|}^{n-2}A$$(A^*)^* = |A|^{n-2} A$

当 $|A|\ne 0$$|A| \neq 0$ 时 (即 A 可逆):

• $A^{\ast }=|A|\cdot A^{-1}$$A^* = |A| \cdot A^{-1}$

• $A=|A|\cdot (A^{\ast }{)}^{-1}$$A = |A| \cdot (A^*)^{-1}$

• $A^{-1}=\frac{A^{\ast }}{|A|}$$A^{-1} = \frac{A^*}{|A|}$

其他重要公式1:

• $(kA)(kA{)}^{\ast }=|kA|\cdot E$$(kA)(kA)^* = |kA| \cdot E$

• $(A^T)(A^T{)}^{\ast }=|A^T|\cdot E$$(A^T)(A^T)^* = |A^T| \cdot E$

• $(A^{-1})(A^{-1}{)}^{\ast }=|A^{-1}|\cdot E$$(A^{-1})(A^{-1})^* = |A^{-1}| \cdot E$

• $(A^{\ast })(A^{\ast }{)}^{\ast }=|A^{\ast }|\cdot E$$(A^*)(A^*)^* = |A^*| \cdot E$

其他重要公式2:

• $(AB{)}^{\ast }=B^{\ast }{A}^{\ast }$$(AB)^* = B^* A^*$

• $(kA{)}^{\ast }=k^{n-1}{A}^{\ast }$$(kA)^* = k^{n-1} A^*$

• $(A^T{)}^{\ast }=(A^{\ast }{)}^T$$(A^T)^* = (A^*)^T$

• $(A^{-1}{)}^{\ast }=(A^{\ast }{)}^{-1}$$(A^{-1})^* = (A^*)^{-1}$

其他重要公式3:

• $(kA{)}^{-1}=\frac{1}{k}{A}^{-1}$$(kA)^{-1} = \frac{1}{k} A^{-1}$

• $(kA{)}^T=k{A}^T$$(kA)^{T} = kA^{T}$

• $|kA|=k^n|A|$$|kA| = k^n|A|$

• $|B^{-1}|=|B{|}^{-1}$$|B^{-1}| = |B|^{-1}$

• $C\cdot C^{\ast }=|C|\cdot E⟹C^{\ast }=|C|\cdot C^{-1}$$C \cdot C^* = |C| \cdot E \implies C^* = |C| \cdot C^{-1}$

注意: $(A+B{)}^{\ast }\ne A^{\ast }+B^{\ast }$$(A+B)^* \neq A^* + B^*$

8. 简单分块矩阵的逆

若 A, B 可逆，则有：

副对角线需换位

分块矩阵行列式 (设 A 为 m 阶，C 为 n 阶):

• $\left|\begin{array}{cc}{A}_m& B\\ O& C_n\end{array}\right|=|A|\cdot |C|$$\begin{vmatrix} A_m & B \\ O & C_n \end{vmatrix} = |A| \cdot |C|$

• $\left|\begin{array}{cc}B& A_m\\ C_n& O\end{array}\right|=(-1{)}^{mn}|A|\cdot |C|$$\begin{vmatrix} B & A_m \\ C_n & O \end{vmatrix} = (-1)^{mn} |A| \cdot |C|$

• $|ABC|=|A|\cdot |B|\cdot |C|$$|ABC| = |A| \cdot |B| \cdot |C|$

9. 二阶矩阵，求伴随，主对换，副反号

对于二阶矩阵 $\begin{array}{c}A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\end{array}$$A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$，其伴随矩阵为 $\begin{array}{c}{A}^{\ast }=\left[\begin{array}{cc}d& -b\\ -c& a\end{array}\right]\end{array}$$A^* = \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}$。

口诀: 主对角线元素互换，副对角线元素变号。

10. 初等矩阵 / 初等变换 (倍乘、互换、倍加)

变换法则: 左行右列

• $E_2(k)$$E_2(k)$ — 第 2 行乘 k 倍

• $E_{12}$$E_{12}$ — 第 1, 2 行互换

• $E_{31}(k)$$E_{31}(k)$ — 第 1 行 k 倍加到第 3 行

初等矩阵的性质: ① 初等矩阵的转置仍是初等矩阵: $E_{ij}^T=E_{ij}$$E_{ij}^T = E_{ij}$, $E_i^T(k)=E_i(k)$$E_i^T(k) = E_i(k)$，$E_{ij}^T(k)=E_{ji}(k)$$E_{ij}^T(k) = E_{ji}(k)$ ② 初等矩阵的逆:

• $E_{ij}^{-1}=E_{ij}$$E_{ij}^{-1} = E_{ij}$

• $E_i^{-1}(k)=E_i(\frac{1}{k})$$E_i^{-1}(k) = E_i(\frac{1}{k})$

• $E_{ij}^{-1}(k)=E_{ij}(-k)$$E_{ij}^{-1}(k) = E_{ij}(-k)$

11. 可逆矩阵与秩

• 可逆矩阵可以表示为有限个初等矩阵的乘积；任何可逆矩阵 P，可以拆解成若干初等阵乘积。

• 若 $|A|\ne 0$$|A| \neq 0$ (即 A 满秩可逆)，则可逆矩阵 $A$$A$ 乘以其他矩阵不改变其秩。

初等变换不改变矩阵的秩

12. 矩阵等价

定义: 矩阵 A 与 B 等价，记作 $A\sim B$$A \sim B$，是指 A 经过有限次初等变换可以化为 B。

充要条件: $r(A)=r(B)$$r(A) = r(B)$

13. 秩的性质 (乘积为零)

若 $A_{m\times n}\cdot B_{n\times s}=O$$A_{m \times n} \cdot B_{n \times s} = O$，则有：

注: 此处的 $n$$n$ 是矩阵 A 的列数（也是矩阵 B 的行数）。

14. 秩的性质 (与初等变换相关)

• $r(A\cdot B)\le r(A)$$r(A \cdot B) \le r(A)$

• 若 P 可逆，则 $r(P\cdot A)=r(A)$$r(P \cdot A) = r(A)$

解释: 对于 $A\cdot B=C$$A \cdot B = C$，C 的列向量可以由 A 的列向量线性表示，C 的行向量可以由 B 的行向量线性表示。

15. 正交矩阵

定义: 若方阵 A 满足 $A{A}^T=A^{T}A=E$$AA^T = A^TA = E$，则称 A 为正交矩阵。

• 等价于 $A^{-1}=A^T$$A^{-1} = A^T$

• 等价于 A 的行（列）向量都是单位向量，且行（列）向量两两正交。

注: 对于一个单位行向量 $(a_1,a_2,\cdots ,a_n)$$(a_1, a_2, \cdots, a_n)$，有 $a_1^2+a_2^2+\cdots +a_n^2=1$$a_1^2 + a_2^2 + \cdots + a_n^2 = 1$。

16. 方阵的多项式运算

方阵的多项式可以像数一样相乘和因式分解。 例: 设 A 为 n 阶矩阵，则：

可以进行因式分解：

注: 此处推导结果为 E，表明 $A$$A$ 与括号内的多项式互为逆矩阵。

17. 幂等矩阵

$A^2=A$$A^2 = A$ 不能推出 $A=E$$A = E$。

反例: 零矩阵 $O$$O$ 和某些非单位的投影矩阵都满足 $A^2=A$$A^2 = A$。

18. 零矩阵的判定

一个矩阵的秩为 0，它的每一个元素都为 0。(显而易见)

19. 秩的综合性质

伴随矩阵的秩: 对于 n 阶矩阵 A，其伴随矩阵 $A^{\ast }$$A^*$ 的秩为：

推论: $r(A_{n\times n})=n⟺|A|\ne 0⟺A\text{ 可逆}$$r(A_{n \times n}) = n \iff |A| \neq 0 \iff A \text{ 可逆}$

其他重要不等式与等式:

• $r(kA)=r(A)$$r(kA) = r(A)$，其中 $k\ne 0$$k \neq 0$

• $r(A)\le r(A,b)$$r(A) \le r(A, b)$，其中 $(A,b)$$(A, b)$ 为 A 的增广矩阵

• $r(AB)\le min\{r(A),r(B)\}$$r(AB) \le \min\{r(A), r(B)\}$

• $r(A+B)\le r(A)+r(B)$$r(A + B) \le r(A) + r(B)$

• $r(A)=r(PA)=r(AQ)=r(PAQ)$$r(A) = r(PA) = r(AQ) = r(PAQ)$，其中 P, Q 为可逆矩阵

• $r(A^T)=r(A)=r(A^{T}A)=r(A\cdot A^T)$$r(A^T) = r(A) = r(A^TA) = r(A \cdot A^T)$

再次强调: 若 $A_{m\times n}\cdot B_{n\times s}=O$$A_{m \times n} \cdot B_{n \times s} = O$，则 $r(A)+r(B)\le n$$r(A) + r(B) \le n$。

注: 此处的 $n$$n$ 是矩阵 A 的列数（也是矩阵 B 的行数）。

三、向量组

1. 内积与正交

设 $\alpha =[{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n{]}^T$$\alpha = [\alpha_1, \alpha_2, \cdots, \alpha_n]^T$, $\beta =[b_1,b_2,\cdots ,b_n{]}^T$$\beta = [b_1, b_2, \cdots, b_n]^T$。

• 内积: $(\alpha ,\beta )={\alpha }^T\beta =\sum _{i=1}^n{a}_i{b}_i=a_1{b}_1+a_2{b}_2+\cdots +a_n{b}_n$$(\alpha, \beta) = \alpha^T \beta = \sum_{i=1}^{n} a_i b_i = a_1b_1 + a_2b_2 + \cdots + a_nb_n$

• 正交向量: 若 ${\alpha }^T\beta =0$$\alpha^T \beta = 0$，则称 $\alpha ,\beta$$\alpha, \beta$ 为正交向量。

• 模 (长度): $||\alpha ||=\sqrt{\sum _{i=1}^n{a}_i^2}$$||\alpha|| = \sqrt{\sum_{i=1}^{n} a_i^2}$。当 $||\alpha ||=1$$||\alpha|| = 1$ 时，$\alpha$$\alpha$ 为单位向量。

正交矩阵: $A^T\cdot A=E⟺A^T=A^{-1}$$A^T \cdot A = E \iff A^T = A^{-1}$

• 标准正交向量组: 若向量组 ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_s$$\alpha_1, \alpha_2, \cdots, \alpha_s$ 中任意两个向量都正交，且每个向量都是单位向量，则称其为标准正交向量组。

  • 即满足：$\begin{array}{c}{\alpha }_i^T{\alpha }_j=\{\begin{array}{ll}0,& i\ne j\\ 1,& i=j\end{array}\end{array}$$\alpha_i^T \alpha_j = \begin{cases} 0, & i \neq j \\ 1, & i = j \end{cases}$

  • 即$({\alpha }_i,{\alpha }_j)=0$$(\alpha_i, \alpha_j) = 0$，$i\ne j$$i \neq j$ $⟺$$\iff$ ${\alpha }_i$$\alpha_i$与${\alpha }_j$$\alpha_j$正交

2. 向量组的线性无关性

若 ${\alpha }_1,{\alpha }_2,{\alpha }_3$$\alpha_1, \alpha_2, \alpha_3$ 线性无关，且 $\beta$$\beta$ 不可由 ${\alpha }_1,{\alpha }_2,{\alpha }_3$$\alpha_1, \alpha_2, \alpha_3$ 线性表示，则 ${\alpha }_1,{\alpha }_2,{\alpha }_3,\beta$$\alpha_1, \alpha_2, \alpha_3, \beta$ 线性无关。

• 此时，秩的关系为：$r({\alpha }_1,{\alpha }_2,{\alpha }_3,\beta )=r({\alpha }_1,{\alpha }_2,{\alpha }_3)+1$$r(\alpha_1, \alpha_2, \alpha_3, \beta) = r(\alpha_1, \alpha_2, \alpha_3) + 1$

3. 秩的性质

若矩阵 A 列满秩（即 $r(A_{m\times n})=n$$r(A_{m \times n}) = n$），则对于任意矩阵 B，有 $r(AB)=r(B)$$r(AB) = r(B)$。

PS: 《1000题》3-5 题考察此知识点，用于证明向量组是否线性无关或可逆

4. 判断向量组的线性相关性

判断向量组 ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n$$\alpha_1, \alpha_2, \cdots, \alpha_n$ 的线性相关性：

• 秩满，线性无关: $r({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)=n⟺{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n$$r(\alpha_1, \alpha_2, \cdots, \alpha_n) = n \iff \alpha_1, \alpha_2, \cdots, \alpha_n$ 线性无关。

• 秩不满，线性相关: $r({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)<n⟺{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n$$r(\alpha_1, \alpha_2, \cdots, \alpha_n) < n \iff \alpha_1, \alpha_2, \cdots, \alpha_n$ 线性相关。

5. 向量组等价

向量组 $⟨I⟩$$\langle I \rangle$ 与 $⟨II⟩$$\langle II \rangle$ 等价，是指它们可以互相线性表示。

• 设向量组 ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_s$$\alpha_1, \alpha_2, \cdots, \alpha_s$ 和 $\beta$$\beta$，则：

  • $r({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_s,\beta )=r({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_s)=s⟺\beta$$r(\alpha_1, \alpha_2, \cdots, \alpha_s, \beta) = r(\alpha_1, \alpha_2, \cdots, \alpha_s) = s \iff \beta$ 可由 ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_s$$\alpha_1, \alpha_2, \cdots, \alpha_s$ 线性表示，且表示法唯一。

  • $r({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_s,\beta )=r({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_s)<s⟺\beta$$r(\alpha_1, \alpha_2, \cdots, \alpha_s, \beta) = r(\alpha_1, \alpha_2, \cdots, \alpha_s) < s \iff \beta$ 可由 ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_s$$\alpha_1, \alpha_2, \cdots, \alpha_s$ 线性表示，但表示法不唯一。

  • $r({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_s)<r({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_s,\beta )⟺\beta$$r(\alpha_1, \alpha_2, \cdots, \alpha_s) < r(\alpha_1, \alpha_2, \cdots, \alpha_s, \beta) \iff \beta$ 不可由 ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_s$$\alpha_1, \alpha_2, \cdots, \alpha_s$ 线性表示。

6. 两向量组等价的判定

向量组 ${\alpha }_1,{\alpha }_2,{\alpha }_3$$\alpha_1, \alpha_2, \alpha_3$ 与 ${\beta }_1,{\beta }_2,{\beta }_3$$\beta_1, \beta_2, \beta_3$ 等价，当且仅当：

大题解法: 写出增广矩阵 $(A,B)$$(A, B)$，验证 $r(A)=r(A,B)$$r(A) = r(A, B)$，并单独验证 $r(B)$$r(B)$，确保三个秩相等。

7. 施密特正交化

若向量组 ${\alpha }_1,{\alpha }_2,{\alpha }_3$$\alpha_1, \alpha_2, \alpha_3$ 线性无关，则可通过施密特正交化方法构造一组两两正交的向量组 ${\beta }_1,{\beta }_2,{\beta }_3$$\beta_1, \beta_2, \beta_3$，且新向量组与原向量组等价。

• 公式:

  • ${\beta }_1={\alpha }_1$$\beta_1 = \alpha_1$

  • ${\beta }_2={\alpha }_2-\frac{({\alpha }_2,{\beta }_1)}{({\beta }_1,{\beta }_1)}\cdot {\beta }_1$$\beta_2 = \alpha_2 - \frac{(\alpha_2, \beta_1)}{(\beta_1, \beta_1)} \cdot \beta_1$

  • ${\beta }_3={\alpha }_3-\frac{({\alpha }_3,{\beta }_1)}{({\beta }_1,{\beta }_1)}\cdot {\beta }_1-\frac{({\alpha }_3,{\beta }_2)}{({\beta }_2,{\beta }_2)}\cdot {\beta }_2$$\beta_3 = \alpha_3 - \frac{(\alpha_3, \beta_1)}{(\beta_1, \beta_1)} \cdot \beta_1 - \frac{(\alpha_3, \beta_2)}{(\beta_2, \beta_2)} \cdot \beta_2$

PS: 线性无关向量组经过施密特正交规范化后，结果不唯一（因为正交化过程中可以选择不同的顺序或归一化方式）。

8. 零向量组的性质

零向量组必然可以被其余任何向量组线性表示。

四、线性方程组

1. 非齐次线性方程组 $Ax=b$$Ax = b$ ($b\ne 0$$b \neq 0$)

有解判定: 线性方程组有解 $⟺r(A)=r(\overline{A})$$\iff r(A) = r(\bar{A})$

注: $\overline{A}=(A,b)$$\bar{A} = (A, b)$ 为增广矩阵。

解的情况:

• 唯一解: $⟺r(A)=r(A,b)=n$$\iff r(A) = r(A, b) = n$ （n 为未知量个数，即 A 的列数）

• 无穷多解: $⟺r(A)=r(A,b)<n$$\iff r(A) = r(A, b) < n$

• 无解: $⟺r(A)<r(A,b)$$\iff r(A) < r(A, b)$ （矛盾方程）

几何意义/向量解释:

• $r(A)=r(A,b)⟺b$$r(A) = r(A, b) \iff b$ 可由 A 的列向量组线性表示。

• $r(A)=r(A,b)⟺b^T$$r(A) = r(A, b) \iff b^T$ 可由 $A^T$$A^T$ 的行向量组线性表示。

• $\begin{array}{c}r(A)=r(A,b)\iff r(A^T)=r\left(\begin{array}{c}{A}^T\\ b^T\end{array}\right)\end{array}$$\quad r(A) = r(A, b) \quad \Leftrightarrow \quad r(A^T) = r\begin{pmatrix} A^T \\ b^T \end{pmatrix}$

2. 齐次线性方程组 $Bx=0$$Bx = 0$

非零解: $Bx=0$$Bx = 0$ 有非零解 $⟺r(B)<n$$\iff r(B) < n$ （n 为未知量个数，即 B 的列数）

注: 此时有效方程个数$r(B)$$r(B)$小于未知量个数。

仅有零解: $Bx=0$$Bx = 0$ 仅有零解 $⟺r(B)=n$$\iff r(B) = n$

3. 方阵行列式与可逆性

对于方阵 A，有：

推论: 设 $A_{m\times n},B_{n\times m}$$A_{m \times n}, B_{n \times m}$，若 $m>n$$m > n$，则有 $r(AB)\le r(A)\le n<m⟹|AB|=0$$r(AB) \le r(A) \le n < m \implies |AB| = 0$

注: 秩越乘越小。

4. 非齐次方程通解

非齐次线性方程组的通解 = 非齐次方程的一个特解 + 对应齐次方程组的通解。

重要性质: 非齐次方程的两个特解之差，必为对应齐次方程组的解。

5. 齐次线性方程组解的条件与结构

设 $A_{m\times n}x=0$$A_{m \times n} x = 0$。

解的情况: ① 当 $r(A)=n$$r(A) = n$（即 A 的列向量线性无关）时，方程组有唯一零解。 ② 当 $r(A)=r<n$$r(A) = r < n$（即 A 的列向量线性相关）时，方程组有无穷多解，且基础解系包含 $n-r$$n - r$ 个线性无关的解向量。

自由度: $n-r$$n - r$ 是“真实的约束个数”的补集。

基础解系: 设 ${\xi }_1,{\xi }_2,\cdots ,{\xi }_{n-r}$$\xi_1, \xi_2, \cdots, \xi_{n-r}$ 满足： ① $A{\xi }_i=0$$A\xi_i = 0$ （是解） ② ${\xi }_1,{\xi }_2,\cdots ,{\xi }_{n-r}$$\xi_1, \xi_2, \cdots, \xi_{n-r}$ 线性无关 ③ $Ax=0$$Ax=0$ 的任意解均可由 ${\xi }_1,{\xi }_2,\cdots ,{\xi }_{n-r}$$\xi_1, \xi_2, \cdots, \xi_{n-r}$ 线性表示 则称 ${\xi }_1,{\xi }_2,\cdots ,{\xi }_{n-r}$$\xi_1, \xi_2, \cdots, \xi_{n-r}$ 为 $Ax=0$$Ax=0$ 的基础解系。

注: 基础解系中向量的个数 $s=n-r(A)$$s = n - r(A)$。

6. 解的线性无关性

$Ax=b$$Ax = b$ 有 s 个线性无关解 $⟺Ax=0$$\iff Ax = 0$ 有 s-1 个线性无关解。

$Ax=b$$Ax = b$ 无关解向量个数为 $n-r(A)+1$$n-r(A)+1$

例: 设 ${\alpha }_1,{\alpha }_2,{\alpha }_3$$\alpha_1, \alpha_2, \alpha_3$ 是 $Ax=b$$Ax=b$ 的 3 个线性无关解，则 ${\alpha }_1-{\alpha }_2,{\alpha }_2-{\alpha }_3$$\alpha_1 - \alpha_2, \alpha_2 - \alpha_3$ 是 $Ax=0$$Ax=0$ 的 2 个线性无关解。

7. 解向量的正交性

向量 $\begin{array}{c}x=\left(\begin{array}{c}{x}_1\\ ⋮\\ x_n\end{array}\right)\end{array}$$x = \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix}$ 是齐次线性方程组 $Ax=0$$Ax=0$ 的解 $⟺x$$\iff x$ 与 A 的任一行向量正交。

8. $A^{T}Ax=0$$A^TAx = 0$ 与 $Ax=0$$Ax = 0$ 同解

PS: 证明见《30讲》习题 4.8。

9. 求解齐次线性方程组的通解

求解 $Ax=0$$Ax=0$ 的通解，需要找到其基础解系，即寻找满足以下三个条件的 s 个向量： ① 是 $Ax=0$$Ax=0$ 的解 ② 线性无关 ③ $s=n-r(A)$$s = n - r(A)$ （个数等于自由变量的个数）

10. 非齐次方程组求通解

步骤: 对增广矩阵 $(A,b)$$(A, b)$ 进行初等行变换，化为行最简形。

示例:

• 自由变量个数: $n-r(A)=4-2=2$$n - r(A) = 4 - 2 = 2$ 个自由变量。

• 约束变量: 抬脚（主元）对应的变量 $x_1,x_2$$x_1, x_2$。

• 自由变量: $x_3,x_4$$x_3, x_4$。

求解过程:

1. 求对应齐次方程组 $Ax=0$$Ax=0$ 的通解:

   • 将自由变量 $x_3,x_4$$x_3, x_4$ 依次赋值 $(1,0)$$(1, 0)$ 和 $(0,1)$$(0, 1)$，得到基础解系。

   • 解得：

     $$\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right)=k_1\left(\begin{array}{c}-2\\ 1\\ 1\\ 0\end{array}\right)+k_2\left(\begin{array}{c}4\\ -5\\ 0\\ 1\end{array}\right)$$

2. 求非齐次方程组 $Ax=b$$Ax=b$ 的一个特解:

   • 将自由变量 $x_3,x_4$$x_3, x_4$ 赋值为 0。

   • 解得特解为：

     $$\left(\begin{array}{c}2\\ -3\\ 0\\ 0\end{array}\right)$$

3. 写出通解:

   • 非齐次方程组的通解 = 特解 + 齐次方程组的通解。

   • 最终通解为：

     $$\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right)=k_1\left(\begin{array}{c}-2\\ 1\\ 1\\ 0\end{array}\right)+k_2\left(\begin{array}{c}4\\ -5\\ 0\\ 1\end{array}\right)+\left(\begin{array}{c}2\\ -3\\ 0\\ 0\end{array}\right)$$

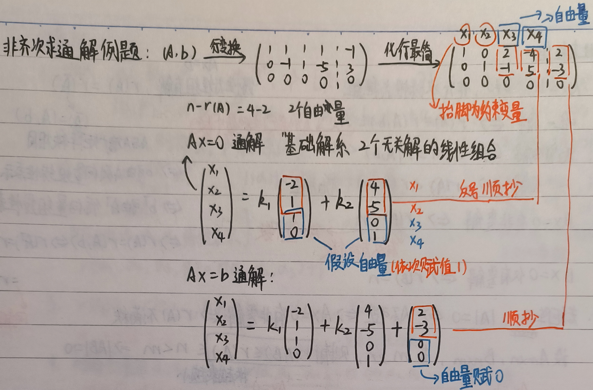
技巧: 在写解向量时，“反号顺抄”指从行最简形中抄写系数时注意符号；“顺抄”指直接抄写特解部分。

10. 初等行变换的性质

初等行变换不改变矩阵列向量间的线性关系。

• 若 $A\stackrel{r}{\to }B$$A \xrightarrow{r} B$，则方程组 $Ax=0$$Ax=0$ 与 $Bx=0$$Bx=0$ 同解。

11. 每行元素之和为常数类型

若 A 为 n 阶矩阵，且其每行元素之和均为常数 $\lambda$$\lambda$，则 $\lambda$$\lambda$ 是 A 的一个特征值，对应的特征向量为 $\left(\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right)$$\begin{pmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{pmatrix}$。

证明: $\begin{array}{c}A\left(\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right)=\left(\begin{array}{c}\sum a_{i1}\\ \sum a_{i2}\\ ⋮\\ \sum a_{in}\end{array}\right)=\left(\begin{array}{c}\lambda \\ \lambda \\ ⋮\\ \lambda \end{array}\right)=\lambda \left(\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right)\end{array}$$A \begin{pmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{pmatrix} = \begin{pmatrix} \sum a_{i1} \\ \sum a_{i2} \\ \vdots \\ \sum a_{in} \end{pmatrix} = \begin{pmatrix} \lambda \\ \lambda \\ \vdots \\ \lambda \end{pmatrix} = \lambda \begin{pmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{pmatrix}$

12. 方程组同解与向量组等价的关系

• 齐次方程组: $Ax=0$$Ax=0$ 与 $Bx=0$$Bx=0$ 同解 $⟺A\stackrel{r}{\to }B$$\iff A \xrightarrow{r} B$ （即 A 经过初等行变换可化为 B）$⟺A,B$$\iff A, B$ 的行向量组等价。

• 转置方程组: $A^{T}x=0$$A^Tx=0$ 与 $B^{T}x=0$$B^Tx=0$ 同解 $⟺A^T\stackrel{r}{\to }{B}^T$$\iff A^T \xrightarrow{r} B^T$ $⟺A,B$$\iff A, B$ 的列向量组等价 $⟺A^T,B^T$$\iff A^T, B^T$ 的行向量组等价。

• 非齐次方程组: $Ax=\alpha$$Ax=\alpha$ 与 $Bx=\beta$$Bx=\beta$ 同解 $⟺(A,\alpha )\stackrel{r}{\to }(B,\beta )$$\iff (A, \alpha) \xrightarrow{r} (B, \beta)$。

• 特殊情形: 若 $Ax=0$$Ax=0$ 与 $\left(\begin{array}{c}A\\ {\beta }^T\end{array}\right)x=0$$\begin{pmatrix} A \\ \beta^T \end{pmatrix} x = 0$ 同解，则 ${\beta }^T$$\beta^T$ 可由 A 的行向量线性表示 $⟺\beta$$\iff \beta$ 可由 $A^T$$A^T$ 的列向量线性表示 $⟺r(A^T)=r(A^T,\beta )$$\iff r(A^T) = r(A^T, \beta)$ 即$A^{T}x=\beta$$A^Tx=\beta$有解。