Matlab 笔记---学习记录
1.11 writed by luwei
本文相关的仓库地址:Matlab入门学习
基础语法
变量注释与运算符
清除终端内容
xxxxxxxxxx31clear all %清除所有变量2clc %清除Command窗口中所有命令3close all; %关闭所有图形窗口,释放内存并清理工作区运算符
xxxxxxxxxx41a 与 A 是两个变量在matlab中创建变量直接赋值对应的数据类型就可以了2+ - * / sqrt开根号3&& 与; || 或4~= 不等于| 算数 | 描述 | 关系 | 逻辑 | 位运算 | 赋值 | ||||
|---|---|---|---|---|---|---|---|---|---|
+ | 加法 | == | 等于 | && | 逻辑与(短路运算) | bitand | 按位与 | = | 赋值 |
- | 减法 | ~= | 不等于 | || | 逻辑或(短路运算) | bitor | 按位或 | += | 加赋值 |
* | 矩阵乘法 | < | 小于 | & | 逐元素逻辑与 | bitxor | 按位异或 | -= | 减赋值 |
.* | 逐元素乘法 | <= | 小于等于 | | | 逐元素逻辑或 | bitcmp | 按位取反 | *= | 乘赋值 |
/ | 矩阵右除 | > | 大于 | ~ | 逻辑非 | bitshift | 位移 | /= | 除赋值 |
./ | 逐元素右除 | >= | 大于等于 | ^= | 幂赋值 | ||||
^ | 矩阵幂 |
特殊运算符:
::生成序列或选择数组的元素;:用于分隔行或命令...:续行符,用于将一个长命令分成多行
注释
xxxxxxxxxx41%单行注释2%{ 3多行注释4%}基本运算
xxxxxxxxxx61s = 'a' %s 是一个字符数组,包含单个字符 'a'2result = abs(a) % 结果为97,ASCAL码3result = char(666) %将数字666转换为其对应的Unicode字符4lengeh(str) %字符串长度5exp(2) % exp函数用于计算自然指数函数,这里表示e的平方6a = b = 666 %把666赋给b再给arand、randi和randn的区别

元胞数组
xxxxxxxxxx51% cell 类似python元组2A = cell(1,6) 3A{2} = eye(3) %生成一个3x3对角线数值为1的单位矩阵4A{5} = magic(5) %生成n阶幻方矩阵5B = A{5}
Note
MATLAB是从1开始的不是从0开始的,这与绝大部分的编程语言不一样。
结构体
xxxxxxxxxx51% 修正 struct 函数的参数格式,将 name 字段值设为元胞数组2books = struct('name', {'Machine Learning', 'data mining'}, 'price', [30 40]);3books.name % 属性4books.name(1) % 返回 cell5books.name{1} % 返回值矩阵操作
矩阵的数学运算
xxxxxxxxxx61A = [1 2 3;4 5 6;7 8 9] %每行元素的分隔符为空格或者逗号2B = A’ %矩阵转秩,行变列,列变行3C = A(:) %按列每个元素依次按行赋值4D = inv(A) % 求矩阵的逆,只有方阵可以求逆5E = zeros(10,5,3) % 三维 十行五列 零矩阵6矩阵 \ 左除 / 右除 矩阵创建、矩阵构造拼接与逻辑矩阵
xxxxxxxxxx391%矩阵的定义和构造2A = [1 2 3 4 5 6] %创建一维数组3B = 1:2:9 %初值 步长 终值,创建一维数组4C = repmat(B,3,1) %repmat 横重复3次,列重复2次 5D = ones(2,4) %生成2行四列全1矩阵 6.* 和 ./ %矩阵元素相乘或除,不是矩阵乘除7
8%矩阵拼接9A = magic(5) %创建一个 5 × 5 的魔方阵,其中每一行、每一列和两个主对角线上的数字的和都相等10B = A(2,3) %取A矩阵第二行第三个11C = A(3,:) % :表示取全部 第三行12D = A(:,4) %取第四列13[m,n] = find(A>20) %把大于20的值按下标将第几行第几列分别存入m和n中14
15% 在矩阵的第二行插入[10 11 12],本质还是矩阵拼接16newRow = [10 11 12];17rowIndex = 2;18A = [A(1:rowIndex-1, :); newRow; A(rowIndex:end, :)];19
20[numRows, numCols] = size(A4) % size语句返回行数列数,矩阵形式21rankA4 = rank(A4) %取矩阵的秩22
23%在 MATLAB 中,logical() 函数用于将输入数据转换为逻辑数组(logical array),逻辑数组的元素仅能是 0 和 1,分别表示 false(假)和 true(真)。24A = [1, 0, 3; 25 0, 5, 6; 26 7, 0, 9];27B = logical(A);28
29%使用逻辑数组来筛选原数组中的元素。例如,假设我们想找出 A 中所有大于 5 的元素:30A = [1, 2, 3; 31 4, 5, 6; 32 7, 8, 9];33B = A > 5; % 生成逻辑矩阵34filteredValues = A(B); % 使用逻辑矩阵筛选35
36% reshape 函数用于重新排列矩阵的元素,以形成具有不同维度的矩阵。37A = [1, 2, 3, 4; 38 5, 6, 7, 8];39B = reshape(A, [4, 2]);% 将 A 变为 4 行 2 列的矩阵查找矩阵中的非零元素
xxxxxxxxxx111查找稀疏矩阵中的非零元素,并打印出它们的值及其所在的行列位置。2A = [0 0 3 0; 1 0 0 1; 0 9 0 0; 2 0 0 0];3
4% 获取非零元素的索引5[row, col, val] = find(A);6
7% 打印结果8fprintf('非零元素及其位置:\n');9for i = 1:length(val)10 fprintf('值: %d, 行: %d, 列: %d\n', val(i), row(i), col(i));11end用矩阵除法求方程组的解
在 MATLAB 中,可以使用矩阵除法对线性方程组进行求解。如果你有一个线性方程组的形式:
其中 \ 来求解。
假设我们有以下线性方程组:
我们可以将其表示为矩阵形式
代码示例:
xxxxxxxxxx101% 定义系数矩阵A和常数向量b2A = [2, 3; 4, 1];3b = [5; 6];4
5% 使用矩阵左除操作符求解方程组6x = A \ b;7
8% 显示结果9disp('方程组的解为:');10disp(x);步骤如下:
定义矩阵:
A是系数矩阵,包含方程的系数。b是常数向量,包含方程右侧的常数。
矩阵左除:
使用
A \ b计算
结果显示:
使用
disp函数显示解。
注意事项:
确保矩阵
通过
rank(A)和rank([A b])可以进一步分析方程组的解的性质。
使用矩阵除法在 MATLAB 中求解线性方程组是一种高效且简洁的方法。只需定义系数矩阵和常数向量,然后使用左除操作符 \ 即可得到解。
逻辑与流程控制
xxxxxxxxxx331if...else...end2for...end3while...end4switch...case...otherwise...end5
6for 循环变量 = 初值:步长:终值7 执行语句18 ...9 执行语句n10end11%步长为1 可以省略12
13while 条件表达式14 执行语句115 ...16 执行语句n17end18
19if 条件表达式20 ...21 语句体22 ...23end24
25switch 表达式(数值和字符串)26 case 数值和字符串127 语句体128 case 数值和字符串229 语句体230 ...31 otherwise32 语句体n33end函数文件和脚本文件
函数文件关键字:function,函数名与文件名一样,需要与脚本文件在同一工作路径下
示例:创建一个简单的函数文件 add.m:
xxxxxxxxxx31function result = add(a, b)2 result = a + b;3end可以在脚本文件中调用该函数文件,例如:sum = add(3, 5); % sum 将为 8
常用函数
复数运算函数表
| 函数名 | 说明 |
|---|---|
| real(z) | 返回复数z的实部 |
| imag(z) | 返回复数z的虚部 |
| angle(z) | 返回复数z的幅角 |
| abs(z) | 返回复数z的模 |
| conj(z) | 返回复数z的共轭复数 |
| complex(a,b) | 以a和b分别作为实部和虚部,创建复数z |
常用数学函数
| 常用函数 | 含义 |
|---|---|
| sin(x) | 正弦函数,以“弧度”为单位 |
| sqrt(x) | 平方根函数 |
| exp(x) | 指数函数 |
| zeros(m,n) | 创建m行n列的零矩阵 |
| ones(m,n) | 创建m行n列的矩阵,矩阵的所有元素为1 |
| size(A) | 计算矩阵A各维尺寸。size(A,1) ; size(A,2); [m1,m2] =size(A) |
| length(A) | 计算矩阵A最大维尺寸 |
| rand(m,n) | 产生m×n阶由0-1之间均匀取值的数值组成的矩阵 |
矩阵函数
| 常用函数 | 含义 |
|---|---|
| det(A) | 计算方阵行列式 |
| rank(A) | 计算矩阵的秩 |
| inv(A) | 求逆矩阵 |
| find(表达式) | 查找符合表达式的元素并返回其下标 |
| max(A) | 数组中各列的最大值 |
| min(A) | 数组中各列的最小值 |
| mean(A) | 数组中各列的平均值 |
| std(A) | 数组中各列的标准差 |
| size(A) | 数组的行列数 |
| length(A) | 数组的最大维数 |
nargin函数,返回接收参数
在MATLAB中,nargin是一个内置函数,用于返回函数实际接收的输入参数的个数。在编写函数时,nargin可以帮助你根据输入参数的个数来决定函数应执行的操作。
xxxxxxxxxx31function drawShape(N)2if nargin == 03 %逻辑代码find函数,返回符合条件的数组下标
xxxxxxxxxx51% find 函数2A = [1, 2, 3; 4, 5, 6; 7, 8, 9]; % 创建一个 3x3 矩阵3indices = find(A > 5); % 找到大于 5 的元素的线性索引4[row, col] = find(A > 5); % 返回大于 5 的元素的行和列索引5indices = find(A > 5, 2); % 找到前两个大于 5 的元素的线性索引floor函数,确保变量是否为整数
floor(N) == N 的作用是确保 N 是一个整数。
具体来说:
floor(N)函数返回不大于N的最大整数(即向下取整)。如果
N已经是整数,那么floor(N)应该等于N本身。如果
N是一个小数或浮点数,floor(N)将取等于N的整数部分,这时floor(N)和N不相等。
因此,floor(N) == N 这个条件用来判断 N 是否为整数。
判断函数isnumeric、isscalar、isempty、isnan
isnumeric(N):检查N是否是数值。
isscalar(N):检查N是否是标量。
isempty(N):检查N是否为空。
isnan(N) :isnan 函数在 MATLAB 中用于检查输入是否为 "Not-a-Number" (NaN) 值。isnan 返回一个逻辑数组,其中包含 true 表示对应位置的元素为 NaN,false 则表示对应位置的元素不是 NaN。
类型转换函数
int2str(N) :将N转换为字符串
str2double :将输入转换为数字
num2str : 用于将数值转换为字符串。这个函数在需要将数值与其它字符串连接或显示时非常有用。
xxxxxxxxxx11disp([num2str(year) ' 是闰年。']);显示函数fprintf、disp
xxxxxxxxxx101% disp函数不返回输出,适合简单的输出2x = 42;3disp('The value of x is:');4disp(x);5
6% fprintf 返回输出的字符数,支持格式字符串7x = 42;8y = 3.14159;9fprintf('The value of x is: %d\n', x);10fprintf('The value of y is: %.2f\n', y);length函数与size函数
xxxxxxxxxx101v = [1, 2, 3, 4, 5]; %计算向量的长度2L = length(v); % L 将为 53M = [1 2 3; 4 5 6]; %计算矩阵的长度4L = length(M); % L 将为 3,因为矩阵的最大维度是3(列数)5str = 'Hello'; %计算字符串的字符数6L = length(str); % L 将为 57
8%size返回每一维度数组的大小9A = [1 2 3; 4 5 6];10dims = size(A); % dims 返回 [2 3],表示A有2行3列错误信息抛出error
打印错误信息
xxxxxxxxxx11error('Input must be a natural number greater than 2.');请求用户输入input
xxxxxxxxxx11n = input('请输入矩阵的行数 n: ');linspace与logspace
xxxxxxxxxx61y = linspace(a, b, n)2linspace 会生成一个行向量,其中包含从 a 到 b 的 n 个均匀分布的点。n可选默认为100。3
4y = logspace(a, b, n)5logspace 会生成 n 个在 10^a 到 10^b 之间均匀分布的数值。6logspace 函数用于生成在对数尺度上均匀分布的数值数组。这在处理指数增长或衰减的情况时尤其有用。MATLAB绘图
MATLAB 进阶绘图_matlab horizontalalignment-CSDN博客
二维平面绘图
数据处理
xxxxxxxxxx41x = 0:0.01:2*pi; %数据赋值2y = sin(x);3figure %建立一个幕布4t = linspace(0, 6*pi, 1000); % 使用linspace创建从0到6π的1000个点绘图设置
xxxxxxxxxx121figure; % 创建新的图形窗口2plot(x,y)3plot(x, y, 'b-'); %plot函数根据给定的x和y坐标绘制图形,'b-'指定使用蓝色实线绘制。4plot(t, y,'r','LineWidth', 1);5% plot(t, y, '--b', 'LineWidth', 2); % 使用虚线和蓝色,线粗为26
7xlim([0 6*pi]); %设置当前坐标轴的x轴范围 8xticks(0:2*pi:6*pi); %设置当前坐标轴x轴上的刻度位置9ylim([0 1.4]); %设置当前坐标轴的y轴范围 10yticks(0.95:0.05:1.05); %设置y轴的刻度为从0.95到1.05,间隔为0.05,刻度位置为0.95, 1.00, 1.0511
12axis([0 0.2 -1.2 1.2]) %x 轴范围:从 0 到 0.2;y 轴范围:从 -1.2 到 1.2,限制 x 轴和 y 轴的显示范围多个图表绘制
xxxxxxxxxx51subplot(2, 2, 1); % 创建2行2列的子图,激活第1个子图2subplot(m, n, p) 3m:网格的行数。4n:网格的列数。5p:指定当前活动图的位置,从左到右、从上到下编号。将多个曲线绘制在同一张图中
xxxxxxxxxx161x = linspace(0, 2*pi, 100); % 从0到2π生成100个点2y1 = sin(x); % 第一条曲线3y2 = cos(x); % 第二条曲线4y3 = sin(2*x); % 第三条曲线5% 一次性绘制所有曲线6plot(x, y1, 'r', x, y2, 'g', x, y3, 'b'); % 'r', 'g', 'b' 为颜色7legend('sin(x)', 'cos(x)', 'sin(2x)'); % 添加图例8
9或者使用hold on;10y1 = sin(x);11plot(x, y1, 'r'); % 绘制第一条曲线12hold on; % 保持当前图形13y2 = cos(x);14plot(x, y2, 'g'); % 绘制第二条曲线15grid on; % 添加网格16hold off; % 释放当前图形绘图颜色参数选项
| 颜色 | 字符 | 颜色 | 字符 |
|---|---|---|---|
| 红 | r | 粉红 | m |
| 绿 | g | 青 | c |
| 蓝 | b | 白 | w |
| 黄 | y | 黑 | k |
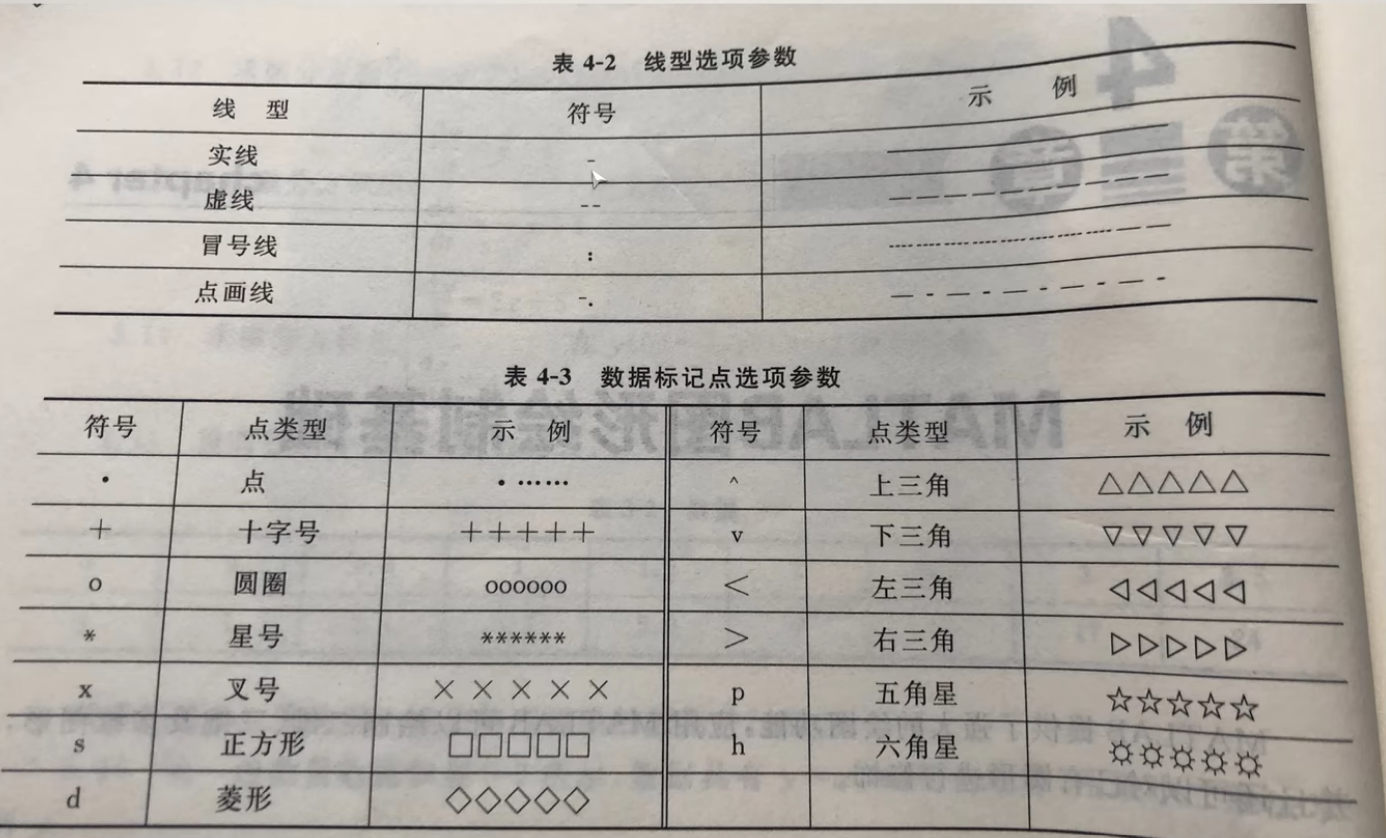
图例标注
xxxxxxxxxx101title('y = sin(x)') %设置标题2sgtitle('Your Title Here') %用于在多个子图的图形窗口中添加一个统一的标题3xlable('x') %在x轴的底部添加标签"x"。4ylable('sin(x)')5
6stem(t_sampled, f_sampled, 'r'); % 采样点,使用 stem 函数绘制,t:时间向量,f采样点的函数值向量7legend('label1', 'label2', ..., 'labelN'); %添加图例,以便为不同的曲线或数据系列提供标签8
9grid on; % 添加网格10axis equal;%axis equal命令设置图形的坐标轴比例,使得单位长度在x轴和y轴方向上相同。xxxxxxxxxx31legend('sin(x)', 'cos(x)', 'sin(2x)', 'Location', 'northeast'); %添加位置参数来自定义图例的位置,'best':自动选择最佳位置2legend('sin(x)', 'cos(x)', 'sin(2x)', 'box', 'off'); % 关闭框线3legend('sin(x)', 'cos(x)', 'sin(2x)', 'FontSize', 12); % 设置 FontSize 属性来更改图例的字体大小不同图形的绘制
xxxxxxxxxx161%具体的图形样式可见下文第三期题目2%柱形图3x = [1 2 5 4 8];4y = [x;1:5];5bar(y,"stacked"); %stacked是一个可选的参数,代表堆栈6barh(y,"stacked"); %barh 水平式的bar7%饼图8a = [15 8 31 46];9pie(a); %画出饼图,自动计算百分比10pie(a,[0,0,0,1]); %画出饼图,并分离第四部分11pie3(a,[1,1,1,1]); %3代表三维12%极坐标图13n = 6;14theta = linspace(0, 2*pi, n+1); % 从 0 到 2\pi 生成 n+1 个点,以便闭合六边形15r = ones(size(theta));%size返回theta向量的元素个数16polar(theta,r);三维图像的绘制
mesh 与 surf
xxxxxxxxxx131x = -3.5:0.2:3.5; % 创建从 -3.5 到 3.5 的 x 数据,步长为 0.22y = -3.5:0.2:3.5; % 创建从 -3.5 到 3.5 的 y 数据,步长为 0.23
4[X,Y] = meshgrid(x,y); % 创建网格矩阵 X 和 Y,适用于二维函数5Z = X .* exp(-X.^2 - Y.^2); % 计算 Z 的值,Z 为 X 和 Y 的复合函数6
7% 绘制网格图8subplot(1,2,1); % 在 1 行 2 列的图形中选择第一个位置9mesh(X,Y,Z); % 绘制网格图10
11% 绘制表面图12subplot(1,2,2); % 选择第二个位置13surf(X,Y,Z); % 绘制表面图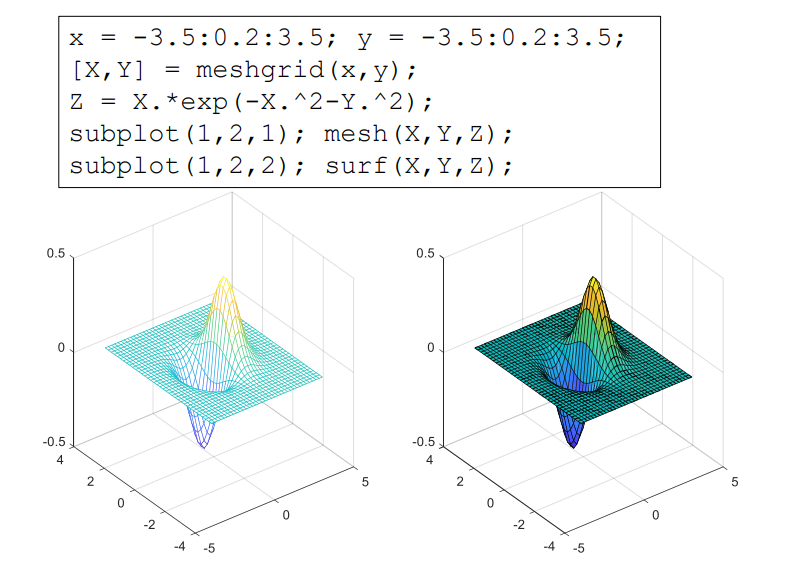
网格图(Mesh Plot):显示了函数 Z 的网格结构,使用线条来表示表面。
表面图(Surface Plot):显示了函数的表面,使用颜色和光泽效果来表示高度信息。
mesh 函数用于绘制三维网格图,它显示了一个网格的线条和表面轮廓。surf 函数用于绘制三维表面图,它不仅显示网格,还通过面填充色彩来表示数据值。
Note
colorbar; % 显示颜色条
shading interp; % 平滑着色
view(45, 30); % 设置观察角度
meshc() 与 surfc()
meshc() 与surfc()是在mesh()和surf()函数的基础上,创建三维网格图,并在底部添加等高线图。
xxxxxxxxxx41x = -3.5:0.2:3.5; y = -3.5:0.2:3.5;2[X,Y] = meshgrid(x,y); Z = X.*exp(-X.^2-Y.^2);3subplot(1,2,1); meshc(X,Y,Z);4subplot(1,2,2); surfc(X,Y,Z);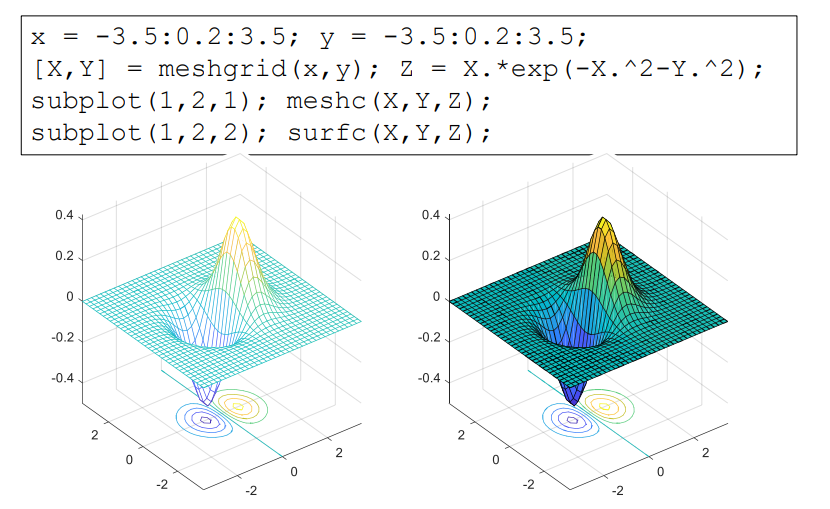
信号产生与处理
考虑生成采样频率为 1000 Hz 的数据。 一个合适的时间矢量是
xxxxxxxxxx181fs = 1000; %fs为采样频率即精度2t = (0:1/fs:1)'; % 0:?:1决定了采样时间为0-1s3%如果有一个矩阵 A 和一个列向量 b,可以使用 A * b 进行矩阵乘法,故通常转换为列向量。4
5y = sin(2*pi*50*t) + 2*sin(2*pi*120*t); % 可以创建由两个正弦波组成的采样信号 y,一个为 50 Hz;另一个为 120 Hz,振幅为原来的两倍。2 * pi * f 是将频率转换为角频率6%在信号中加入正态分布的白噪声,并绘制前 50 个点的曲线7noise = 0.5 * randn(size(y)); % 生成标准差为0.5的高斯白噪声8y_noisy = y + noise; % 将噪声添加到信号中9figure;10plot(t(1:50), y_noisy(1:50), 'b-o'); % 绘制带噪声的信号11hold on;12plot(t(1:50), y(1:50), 'r--'); % 绘制原始信号13xlabel('Time (s)');14ylabel('Amplitude');15title('Signal with Added White Noise (First 50 Points)');16legend('Noisy Signal', 'Original Signal'); % 添加图例17grid on;18hold off;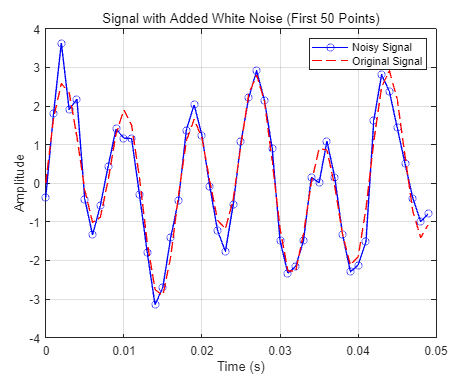
产生 1.5 秒钟的 50 Hz锯齿波(分别为方波),采样率为 10 kHz,同理如下
xxxxxxxxxx51fs = 10000; %采样频率10k2t = (0:1/fs:1.5)'; % 0:?:1.5决定了采样时间为0-1.5s3x = square(2*pi*50*t); %占空比不填默认是50% x = square(2*pi*50*t,80);%占空比为80。4plot(t,x)5axis([0 0.2 -1.2 1.2]) %框定画图范围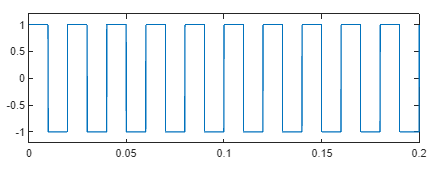
常用的信号函数,使用方法同理
xxxxxxxxxx111t --> 2*pi*f*t1 f频率,t1是个列向量,决定了采样间隔和采用时间2y = sawtooth(t, width) %生成锯齿波信号 width:可选参数,定义波形的上升或下降斜率,0.5 表示生成三角波3y = square(t, duty) %生成方波信号 duty:可选参数,定义方波的占空比(0到100之间,默认值为50)4y = tripuls(t, width) %生成三角脉冲信号 width:可选参数,定义脉冲的宽度(单位时间的比例,默认值为1)5y = rectpuls(t, width) %生成矩形脉冲信号 width:可选参数,定义脉冲的宽度(单位时间的比例,默认值为1)6%若取脉宽为20ms,width取值为20e-37y = gauspuls(t, fc, bw) %生成高斯脉冲信号 fc:中心频率(Hz)bw:带宽(可选,单位为赫兹,默认为1)8
9x = -10:0.01:10; % 输入向量10y = sinc(x) %生成 sinc 函数,通常用于信号处理11plot(x, y);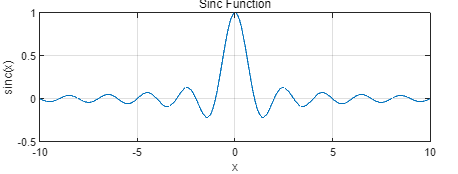
添加高斯噪声
xxxxxxxxxx21noise = sqrt(variance) * randn(size(A)); % 生成高斯白噪声,variance为噪声的方差2A_wnoise = A + sqrt(variance)*randn(size(A)); %输出信号去除信号的线性趋势
detrend 函数可以从信号中去除线性趋势。
示例 1:去除线性趋势
xxxxxxxxxx171% 生成示例信号(例如,带有线性趋势的正弦波)2t = 0:0.01:10; % 时间向量3original_signal = sin(t) + 0.5*t; % 原始信号(带线性趋势)4% 使用 detrend 去除线性趋势5detrended_signal = detrend(original_signal);6% 绘图7figure;8subplot(2,1,1);9plot(t, original_signal, 'b');10title('Original Signal with Linear Trend');11xlabel('Time');12ylabel('Signal Value');13subplot(2,1,2);14plot(t, detrended_signal, 'r');15title('Detrended Signal (Linear Trend Removed)');16xlabel('Time');17ylabel('Signal Value');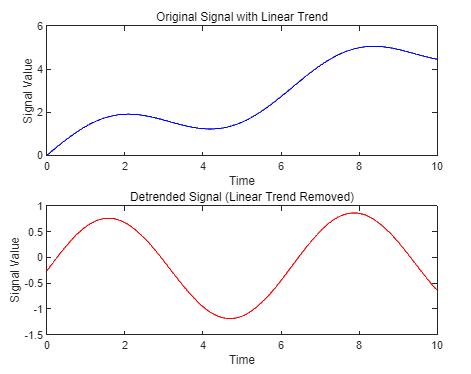
示例 2:去除多项式趋势,去除非线性趋势可以使用多项式拟合,然后从原始信号中减去拟合的非线性趋势。
xxxxxxxxxx201% 生成示例信号(例如,带有非线性趋势的正弦波)2t = 0:0.01:10; % 时间向量3original_signal = sin(t) + 0.2*t.^2; % 原始信号(带非线性趋势)4% 使用 polyfit 拟合二次多项式5p = polyfit(t, original_signal, 2); % 拟合二次多项式6trend_line = polyval(p, t); % 计算趋势线7% 去除多项式趋势8detrended_signal = original_signal - trend_line;9% 绘图10figure;11subplot(2,1,1);12plot(t, original_signal, 'b', t, trend_line, 'r--');13title('Original Signal with Nonlinear Trend');14xlabel('Time');15ylabel('Signal Value');16subplot(2,1,2);17plot(t, detrended_signal, 'r');18title('Detrended Signal (Nonlinear Trend Removed)');19xlabel('Time');20ylabel('Signal Value');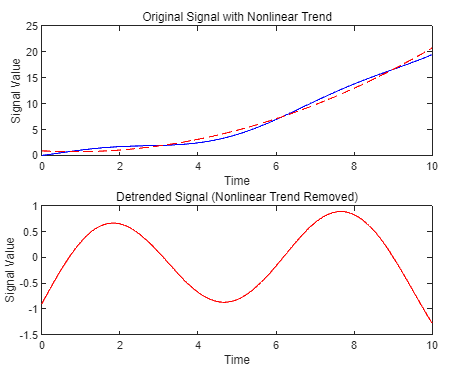
数据拟合与趋势分析
polyfit 函数用于拟合多项式模型。
xxxxxxxxxx51p = polyfit(x, y, n) 2%x:自变量数据(输入向量)多为时间向量3%y:因变量数据(输出向量)多为需要拟合的原始信号4%n:多项式的阶数。5%p:返回的多项式系数向量,按降幂排列。polyval 函数用于计算多项式在给定点的值。它的基本语法是:
xxxxxxxxxx41y_fit = polyval(p, x_fit)2%p:多项式系数向量(由 polyfit 返回)3%x_fit:需要计算的自变量数据。多为时间向量t4%y_fit:返回的多项式在 x_fit 处的值。这两个函数结合使用可以方便地进行数据拟合和趋势分析。
题目
第一期--数组与矩阵
1.已知变量t的取值范围为 0~2π
–产生以π/4为步长的行向量t1;
–利用函数linspace函数产生10个元素的行向量t2;
–求y1 = sin(t1), y2 = cos(t2);
–将y1中小于0的数去除,将y2中小于0的数替换为0;
xxxxxxxxxx61t1 = 0:pi/4:2*pi; 2t2 = linspace(0, 2*pi, 10);%(起始值 终值 元素个数)均分3y1 = sin(t1); 4y2 = cos(t2); 5y1(y1<0)=[]; %将y1中小于0的数去除6y2(y2<0)=0; %将y2中小于0的数替换为02.矩阵操作

xxxxxxxxxx161% PUT YOUR CODE HERE2A0 = zeros(3,4) %产生全零矩阵3A1 = A04A1(1,:)=[1 2 3 4] %改写第一行5
6A2 = A1; 7A2(2,:) = [0 1 1 0]; %改写第二行8A2(3,:) = [0 1 1 0]; 9A3 = A2(:, [1 2 4]); %本质是取出几列赋值到新矩阵里10A4 = [A3; [5 6 7]];11% A = [A; newRow]; % 追加到矩阵末尾12
13[numRows, numCols] = size(A4); %矩阵的函数和列数14maxValues = max(A4, [], 2) % 返回一个列向量,表示每一行的最大值,2表示按行维度进行比较,1为列。15maxValues = min(A4, [], 2)16rankA4 = rank(A4); %求矩阵的秩3.矩阵产生

xxxxxxxxxx61A=[1 2 3;4 5 6;7 8 9]2B=[11 22 33;44 55 66; 77 88 99]3a=A([1:2],[1:3]) % : 冒号表示范围4b=B([2:3],[1,2,3]) % 选定列用`,`也可以用空格5C=[a,b] %等价写法 C=[a b],表示按行拼接6D=[a;b] %表示按列拼接4.用“from : step : to”方式得到从0~4π步长为0.4π的变量X1;用linspace函数得到0~4π分成10点的变量X2;
xxxxxxxxxx21X1 = 0:0.4*pi:4*pi %起始值 步长 终值2X2 = linspace(0, 4*pi, 10) %起始值 终值 等分个数 生成的是行矩阵5.输入矩阵
y\left( x \right) =\left{ \begin{array}{c} \cos x, x\leqslant 0\ -x-x^2, 0<x\leqslant 3\ e^x+2\sqrt{x}, x>3\ \end{array} \right. $$
xxxxxxxxxx91function y = calculate(x)2 if x <= 03 y = cos(x);4 elseif x > 0 && x <= 35 y = -x - x^2;6 else7 y = exp(x) + 2 * sqrt(x);8 end9end第三期--平面绘图
1.在[0,6π]区间内,绘制曲线 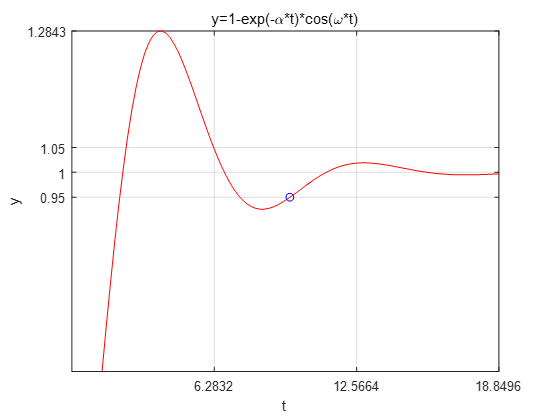
xxxxxxxxxx221% put your code here2% 参数定义3alpha = 0.3;4beta = 0.7;5% 定义时间范围6t = linspace(0, 6*pi, 1000); % 使用linspace创建从0到6π的1000个点7% 计算y值8y = 1 - exp(-alpha * t) .* cos(beta * t);9% 绘制曲线10figure; % 创建新的图形窗口11plot(t, y,'r','LineWidth', 1);12% plot(t, y, '--b', 'LineWidth', 2); % 使用虚线和蓝色,线粗为213xlabel('t');14ylabel('y');15title('y = 1 - exp(-\alpha t) \cdot cos(\beta t)');16
17xlim([0 6*pi]); 18xticks(0:2*pi:6*pi); 19ylim([0 1.4]); 20yticks(0.95:0.05:1.05); 21
22grid on; % 添加网格实际运行图: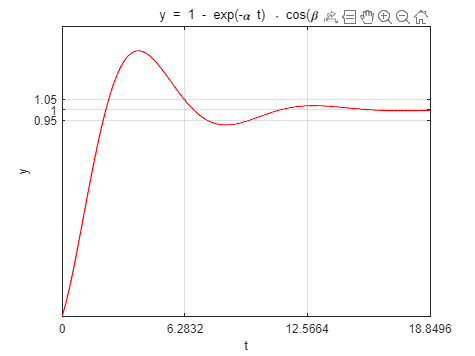
2.Stack the horizontal bar chart.堆叠水平条形图。
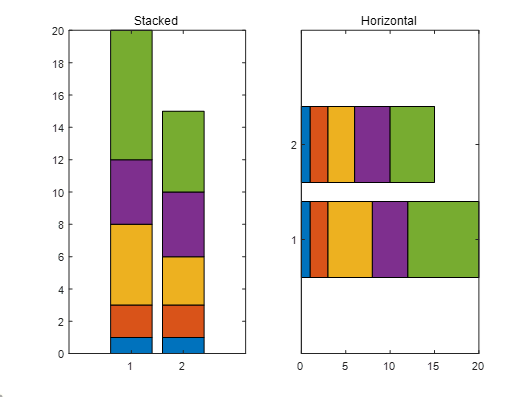
xxxxxxxxxx101% put your code here2clear;clc;close all;3x = [1 2 5 4 8];4y = [x;1:5];5subplot(1,2,1);6bar(y,"stacked"); %stacked是一个可选的参数,代表堆栈7title("Stacked");8subplot(1,2,2);9barh(y,"stacked"); %barh 水平式的bar10title("Horizontal")实际运行图: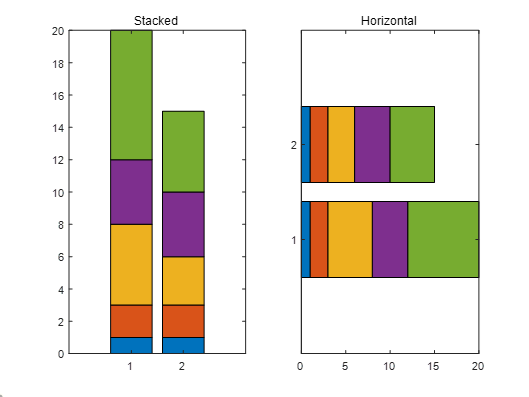
3.Separate all the pieces in the 3D pie chart
分离 3D 饼图中的所有部分
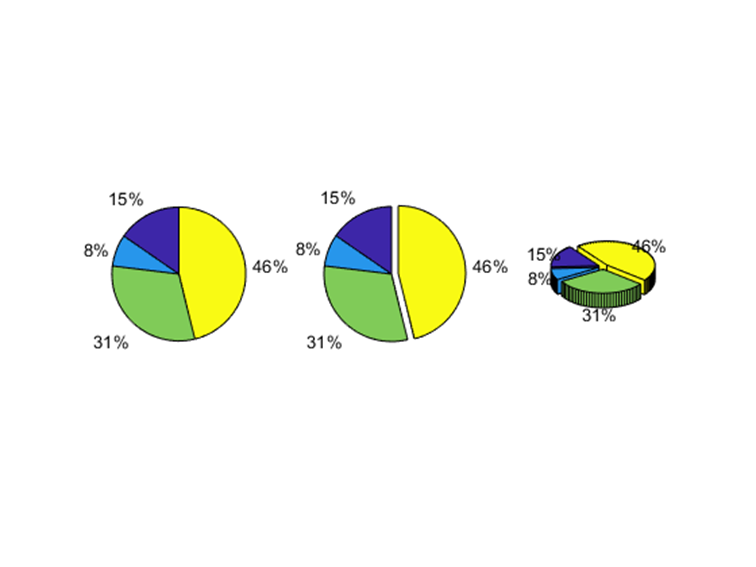
xxxxxxxxxx91% put your code here2clear;clc;close all;3a = [15 8 31 46];4subplot(1,3,1);5pie(a); %画出饼图,自动计算百分比6subplot(1,3,2);7pie(a,[0,0,0,1]);8subplot(1,3,3);9pie3(a,[1,1,1,1]); %3代表三维实际运行图: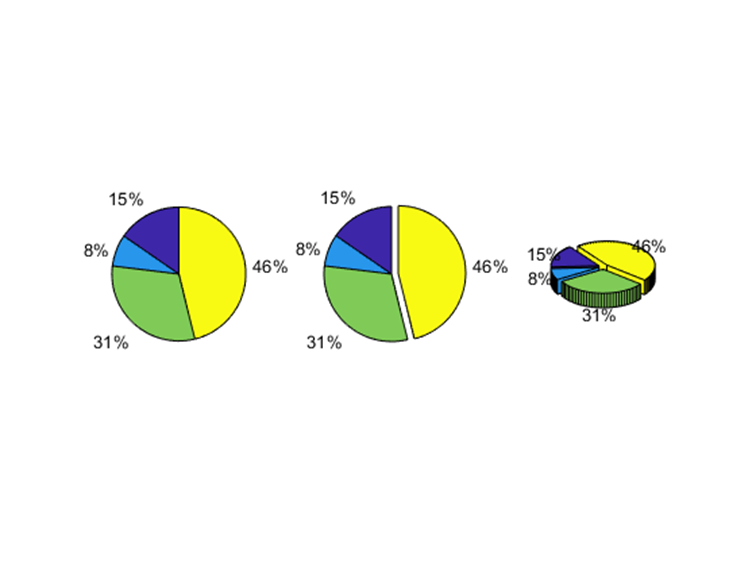
4.Plot a hexagon on a polar chart
在极坐标图上绘制六边形
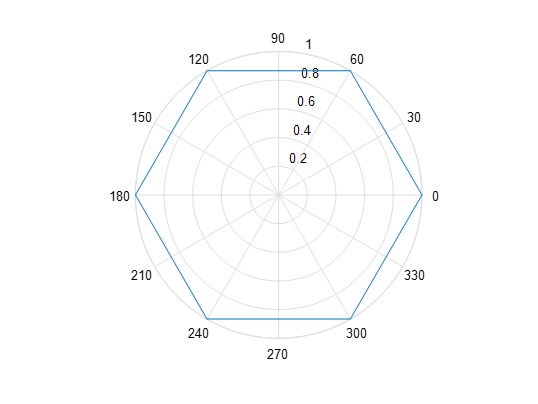
xxxxxxxxxx221% put your code here2% 六边形的边数3n = 6;4% 定义六边形的顶点角度5theta = linspace(0, 2*pi, n+1); % 从 0 到 2\pi 生成 n+1 个点,以便闭合六边形6% 为这些顶点定义半径(1表示正六边形)7r = ones(size(theta));%size返回theta向量的元素个数8% 创建极坐标图9figure;10polar(theta,r);11% 添加图形标题12title('极坐标图上的六边形');13
14%另一种解法15%polarplot(theta, r, '-b', 'LineWidth', 1);16%rlim([0 1]); % 设置 r 轴范围为 0 到 117%rticks(0:0.2:1); % 设置 r 轴刻度为 0, 0.2, 0.4, ..., 118
19%polarplot 是用于绘制极坐标图的 MATLAB 函数。20%theta 和 r 分别指定了每个点的角度和半径。21%- 表示用实线连接顶点,b表示蓝色线型。22%'LineWidth', 1 设置了线条的宽度,使图形更清晰。实际运行图: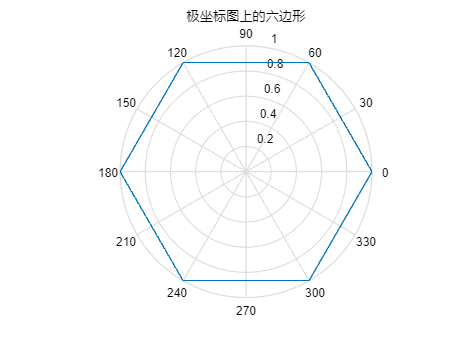
5.Plot a function:stem()绘制函数图:stem() 添加以 5 Hz 频率采样的点
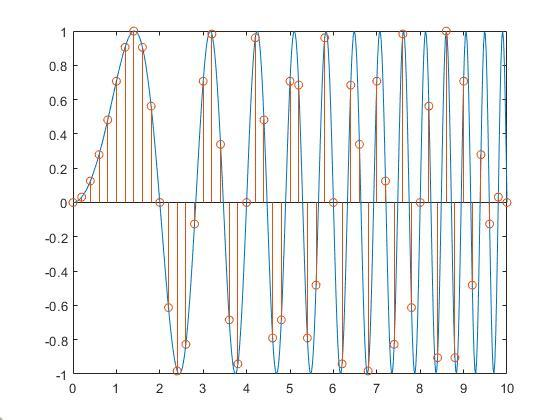
xxxxxxxxxx361% put your code here2% 定义时间范围和步长3t_continuous = linspace(0, 10, 1000); % 连续时间向量,用于绘制平滑曲线4t_sampled = 0:0.2:10; % 以 5 赫兹采样,即每秒 5 个样本,步长为 1/5 = 0.2 秒5
6% 计算连续函数值7f_continuous = sin(pi * t_continuous.^2 / 4);8
9% 计算采样点的函数值10f_sampled = sin(pi * t_sampled.^2 / 4);11%.^ 是用于数组元素逐元素幂运算的运算符12
13% 绘制图形14figure;15plot(t_continuous, f_continuous, 'b-', 'LineWidth', 0.8); % 连续函数曲线16hold on;17%hold on 命令用于保持当前图形窗口活跃,使新的绘图命令不会删除当前的图形内容。在调用 hold on 之后,任何新图形元素(如线条、点或其他图表)都将被添加到现有图形上,而不是替换它们。18stem(t_sampled, f_sampled, 'r'); % 采样点,使用 stem 函数绘制19hold off;20%hold off 命令用于关闭保持状态,恢复默认的图形绘制行为。21
22% 添加标签和标题23xlabel('Time (s)');24ylabel('f(t)');25title('Function f(t) = sin(\pi t^2 / 4) with 5 Hz Sampling Points');26%legend('Continuous Function', 'Sampled Points');%添加图例27%在调用 legend 函数时,顺序很重要。第一个参数 'Continuous Function' 对应 plot 绘制的连续曲线,第二个参数 'Sampled Points' 对应 stem 绘制的采样点28
29% 设置 x 轴范围和刻度30xlim([0 10]); % 设置 x 轴显示范围为 1 到 1031xticks(1:1:10); % 设置 x 轴刻度为 1 到 10,间隔为 132
33ylim([-1 1]); 34yticks(-1:0.2:1); 35
36grid on;实际运行图: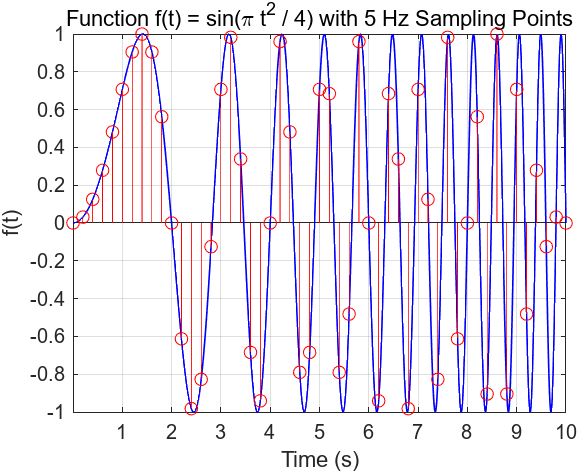
6.Various Contour PlotsCombine the contour techniques to generate a figure as shown below.
各种等高线图将等高线技术相结合,生成如下图所示的图形。
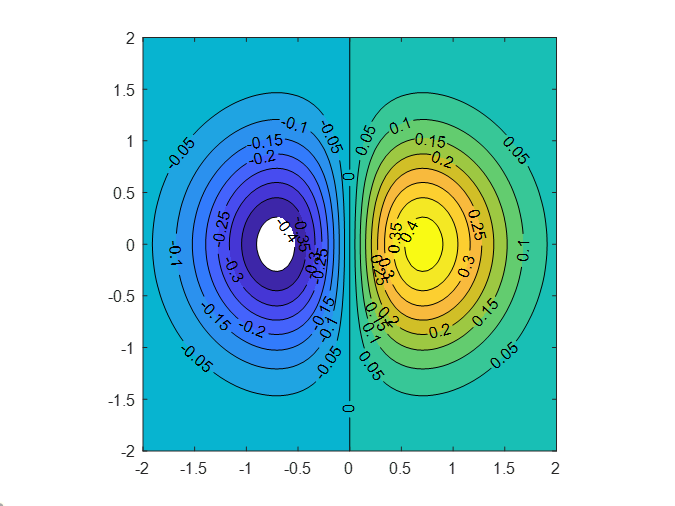
xxxxxxxxxx91% put your code here2x = -2:0.01:2; 3y = -2:0.01:2; 4[X,Y] = meshgrid(x,y);% 创建网格矩阵 X 和 Y,适用于二维函数5Z = X.*exp(-X.^2-Y.^2);% 计算 Z 的值,Z 为 X 和 Y 的复合函数6[C,h] = contourf(X,Y,Z,-.45:.05:.45); % 生成等高线7clabel(C,h);% 添加标签8colormap(jet); % 设置颜色映射为 jet9axis square; %axis square 函数用于调整当前坐标轴的比例,使得 x 轴和 y 轴的单位长度相等实际运行图: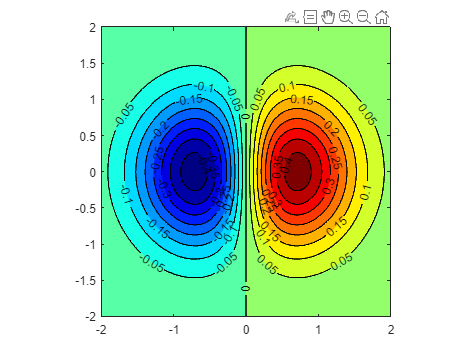
7.Consider two electrocardiogram (ECG) signals with different trends. Load the signals and plot them.
考虑两个趋势不同的心电图(ECG)信号。 加载信号并绘制曲线。
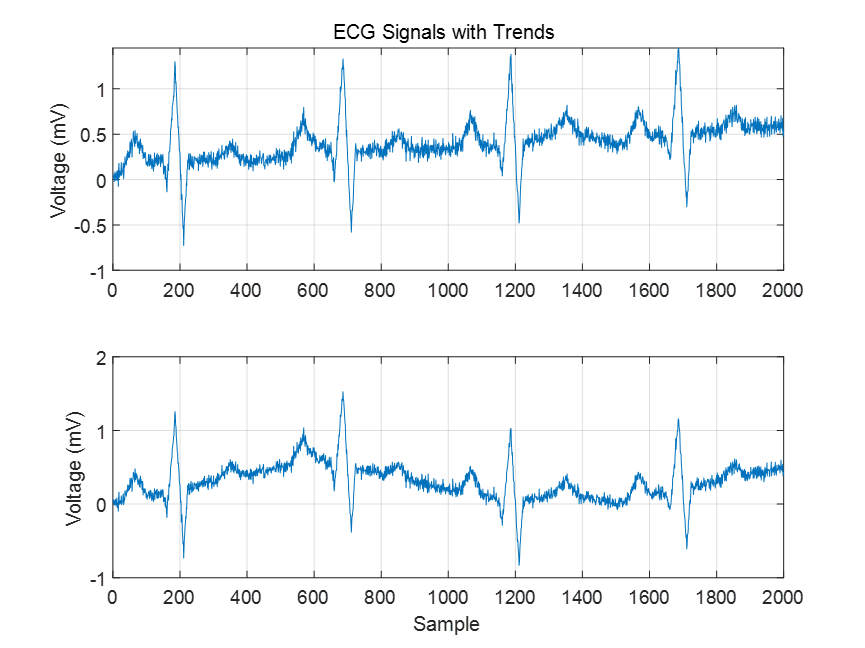
xxxxxxxxxx451% put your code here2load('ecgSignals.mat') %加载同路径下的数据文件3
4% 检查加载的数据结构5whos; % 显示工作区中的变量信息6
7% 假设数据加载后包含两个信号变量 signal1 和 signal28% 根据实际的变量名称和数据结构进行调整9signal1 = ecgl;10signal2 = ecgnl;11
12% 两个信号的采样频率相同,获取信号长度13N = length(signal1); % 信号长度14fs = 1; % 采样频率15
16% 生成时间向量17t = (0:N-1) / fs;18%N-1 的使用是因为 MATLAB 中的索引是从 1 开始的,而信号的采样点是从 0 计数的19
20% 绘制信号21figure;22subplot(2, 1, 1);23plot(t, signal1);24title('ECG Signal 1');25xlabel('Time');26ylabel('Voltage');27grid on;28xlim([0 2000]); 29xticks(0:200:2000); 30ylim([-1 2]); 31yticks(-1:1:2); 32
33subplot(2, 1, 2);34plot(t, signal2);35title('ECG Signal 2');36xlabel('Time');37ylabel('Voltage');38grid on;39xlim([0 2000]); 40xticks(0:200:2000); 41ylim([-1 2]); 42yticks(-1:1:2); 43
44% 调整图形窗口的布局45sgtitle('Comparison of Two ECG Signals');实际运行图: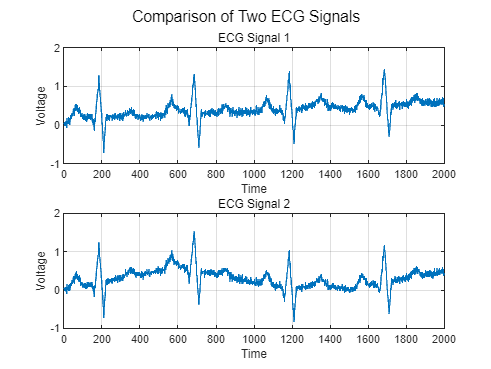
第四期--信号产生
1.Generates 10 seconds of a square wave with a period of π, set the sample rate to 1 kHz and specify a duty cycle of 30%. Add white Gaussian noise with a variance of 1/100 .
产生 10 秒钟的方波,周期为π,设置采样率为 1 kHz,占空比为 30%。 添加方差为 1/100 的白高斯噪声。
xxxxxxxxxx241% 设置参数2fs = 1000; % 采样率 1 kHz3T = pi; % 周期为π4duration = 10; % 信号持续时间 10 秒5dutyCycle = 30; % 占空比 30%6% 生成时间向量7t = 0:1/fs:duration; % 从 0 到 10 秒,间隔为 1/fs8% 生成方波信号9x = square(2 * pi / T * t, 30); % 根据周期和占空比生成方波10% 添加高斯白噪声11variance = 1/100; % 噪声的方差12noise = sqrt(variance) * randn(size(x)); % 生成高斯白噪声13x_noisy = x + noise; % 将噪声添加到方波信号中14% 绘制结果15figure;16plot(t, x_noisy, 'b', 'LineWidth', 1.5); % 绘制带噪声的方波信号17hold on;18plot(t, x, 'r--', 'LineWidth', 1.5); % 绘制原始方波信号19xlabel('Time (s)');20ylabel('Amplitude');21title('Square Wave with Added Gaussian Noise');22legend('Noisy Signal', 'Original Signal');23grid on;24hold off;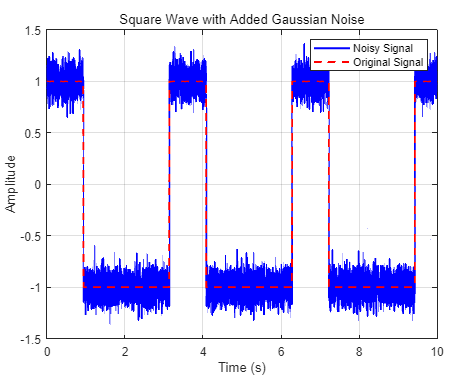
第五期--信号趋势去除与数据拟合
1.Remove Linear Trends from Data
此示例说明如何从股票每日收盘价中去除线性趋势,以重点观察整体涨幅的价格波动。如果数据确实有趋势,则去除线性趋势会强制其均值为零并减少总体变化。该示例使用从 gallery 函数获取的分布来模拟股价波动。 创建一个模拟数据集并计算其均值。sdata 表示股票的每日价格变动。
xxxxxxxxxx31t = 0:300;2dailyFluct = gallery('normaldata',size(t),2); 3sdata = cumsum(dailyFluct) + 20 + t/100;求出数据的平均值。
xxxxxxxxxx11mean(sdata)绘制和标记数据。可以看到,数据显示股价呈系统性增长,效果图如图所示
xxxxxxxxxx51figure2plot(t,sdata);3legend('Original Data','Location','northwest');4xlabel('Time (days)');5ylabel('Stock Price (dollars)');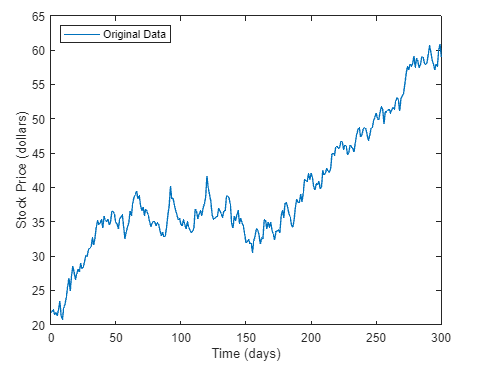
应用 detrend,它对 sdata 执行线性拟合,然后对其进行去除线性趋势处理。从输入中减去输出,得出计算所得的趋势线。
xxxxxxxxxx21detrend_sdata = detrend(sdata);2trend = sdata - detrend_sdata;求出去除线性趋势后的数据的平均值。
xxxxxxxxxx11mean(detrend_sdata)去除线性趋势后,数据均值非常接近 0,与预期相符。 将趋势线、去除线性趋势后的数据及其均值添加到图中,以显示结果。效果如图所示。
xxxxxxxxxx81hold on2plot(t,trend,':r')3plot(t,detrend_sdata,'m')4plot(t,zeros(size(t)),':k')5legend('Original Data','Trend','Detrended Data',...6 'Mean of Detrended Data','Location','northwest')7xlabel('Time (days)'); 8ylabel('Stock Price (dollars)');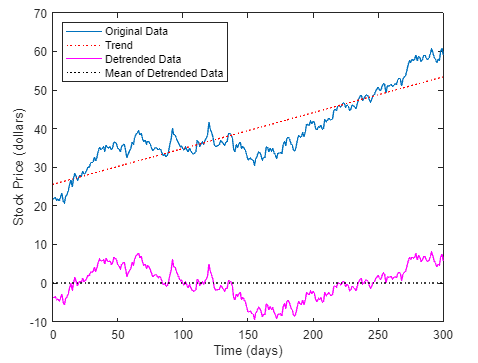
2.Fit Polynomial to Set of Points 将多项式拟合到点集
Create a vector of 5 equally spaced points in the interval [1,2], and evaluate at those points.
在区间 [1,2] 内创建由 5 个等距点组成的向量,并在这些点上求值。
xxxxxxxxxx31points = linspace(1, 2, 5); % 在区间 [1, 2] 中生成5个均匀分布的点2f = @(x) x.^2; % 定义函数3evaluated_values = f(points); % 计算函数值Fit a polynomial of degree 4 to the 5 points. In general, for n points, you can fit a polynomial of degree n-1 to exactly pass through the points.在 5 个点上拟合一条阶数为 4 的多项式。 一般来说,对于 n 个点,可以拟合出一个 n-1 度的多项式来精确通过这些点。
xxxxxxxxxx11p = polyfit(points, evaluated_values, 4); % 拟合4次多项式Evaluate the original function and the polynomial fit on a finer grid of points between 1 and 3.在 1 至 3 点之间的更细网格上评估原始函数和多项式拟合。
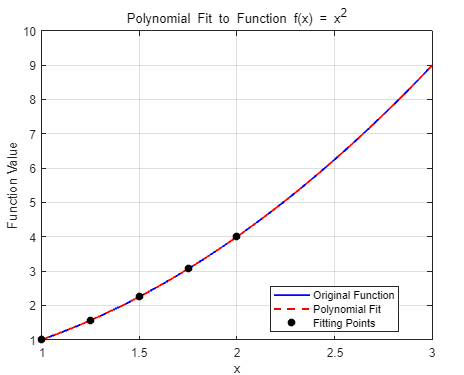
xxxxxxxxxx31fine_grid = linspace(1, 3, 100); % 在区间 [1, 3] 内生成100个点2f_original = f(fine_grid); % 计算原始函数值3f_polyfit = polyval(p, fine_grid); % 计算多项式拟合值Plot the function values and the polynomial fit in the wider interval [1,3], with the points used to obtain the polynomial fit highlighted as circles. The polynomial fit is good in the original [1,2] interval, but quickly diverges from the fitted function outside of that interval.在更宽的区间 [1,3] 内绘制函数值和多项式拟合图,并用圆圈标出用于获得多项式拟合的点。 在原始区间 [1,2] 内,多项式拟合效果良好,但在该区间外,拟合函数迅速发散。
xxxxxxxxxx111figure;2plot(fine_grid, f_original, 'b-', 'LineWidth', 1.5); % 原始函数3hold on;4plot(fine_grid, f_polyfit, 'r--', 'LineWidth', 1.5); % 多项式拟合5plot(points, evaluated_values, 'ko', 'MarkerFaceColor', 'k'); % 拟合点6xlabel('x');7ylabel('Function Value');8title('Polynomial Fit to Function f(x) = x^2');9legend('Original Function', 'Polynomial Fit', 'Fitting Points', 'Location', 'Best');10grid on;11hold off;