通信原理学习笔记
writed by luwei 6-21-23 2025
| 章节 | 重要程度 | 题型 | 考点 |
|---|---|---|---|
| 第一课:绪论 | 选择题 | 信息及其度量、有效性和可靠性 | |
| 第二课:确知信号 | 填空题 | 能量谱和功率谱、自相关函数、互相关函数 | |
| 第三课:随机过程 | 选择题 | 狭义平稳和广义平稳、高斯随机过程一维概率密度函数 | |
| 第四课:信道 | 分析题 | 恒参 | |
| 第五课:模拟调制系统 | 填空题 | 幅度调制、角度调制、功率和带宽的计算 | |
| 第六课 : 数字信带传输系统 | 分析题/计算题 | 无码间干找、码型转换、最佳判决门限和误码率计算 | |
| 第七课 : 数字带通传输系统 &新型数字带通调制技术 | 填空题/计算题 | 二进制数字调制、正交振幅调制、带宽和频带利用率的计算 | |
| 第八课 : 数字信号最佳接收 | 选择题/分析题 | 最佳接收结构、最佳接收原则 | |
| 第九课 : 信源编码 | 填空题/计算题 | 抽样定理、量化信噪比 | |
| 第十课 : 差错控制编码 | 填空题/计算题 | 监督矩阵、生成矩阵 |
离散消息的信息量
设某离散消息
信息量的单位与对数的底
对于等概信源, 二进制的每个码元含
离散消息的平均信息量
设离散信源为:
则该信源中每个符号所含的平均信息量(又称熵)为:
熵的意义:表示信源的不确定性。当每个符号等概率
信息速率与传码率的关系
(1)信息速率与传码率的关系
传码率(波特率)
信息速率(比特率)
进制数 M:对于 M 进制系统,每个码元携带的信息量为
公式推导: 总信息量 = 码元数
(2)误码率
物理意义:传输过程中错误码元数占总码元数的比例,反映系统可靠性。
公式:
确知信号
功率信号:功率有限(一般为周期信号)
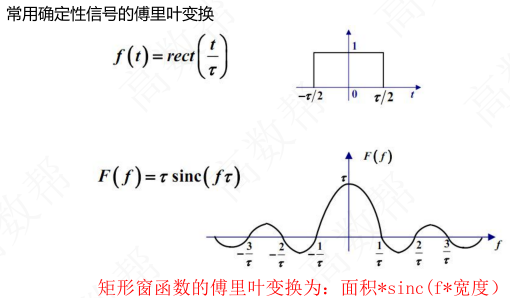
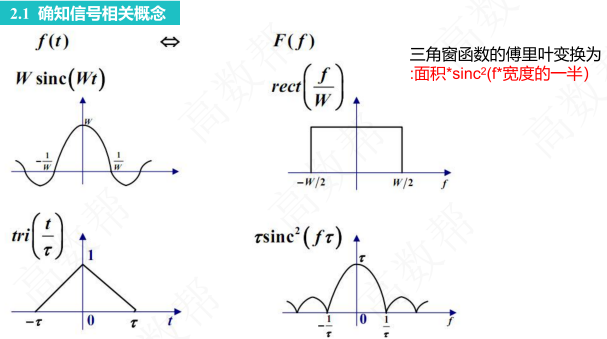
平稳过程的自相关函数
1. 自相关函数的定义
公式:
其中
物理意义:
自相关函数衡量信号在不同时刻的“相似性”。例如:
当
当
通俗理解:
想象一段音乐波形:自相关函数告诉你,如果现在有一个音符,你能多好地预测几秒后的音符。如果波形重复(如鼓点节奏),
2. 自相关函数的性质与物理量解析
(1)
物理量:
为什么是平均功率?
在信号处理中,任何信号
例如:如果
关键点:
对平稳过程,
(2)
物理意义:
自相关函数是偶函数,即关于
通俗理解:
信号在“向前
录音中,向前 2 秒和向后 2 秒的波形相似性一致(平稳过程的特性)。
应用:简化计算,只需分析
(3)
公式修正:
物理意义:
自相关函数在
通俗理解:
信号与自身的相关性(
例如:天气预报中,今天的温度与明天相关性高(
(4)
物理量:
为什么?
当
直流功率对应信号中不随时间变化的“背景值”。
例子:
若
(5)
物理量:
为什么?
总功率
由概率论:
因此,
通俗理解:
总功率 = 直流功率(恒定部分)+ 交流功率(波动部分)。
例如:灯泡的总亮度(总功率)= 基础亮度(直流)+ 闪烁强度(交流)。方差
(6) 当均值为 0 时,
公式:若
物理意义:
均值
3.广义平稳随机过程的性质
高斯随机变量与概率密度函数
(1)高斯随机变量的定义
若随机变量 X 的概率密度函数满足:
(2)线性变换下正态分布的不变性
性质:若
推导逻辑:
可通过 “分布函数法” 或 “特征函数法” 证明:
分布函数法:先求 Y 的分布函数
特征函数法:正态分布的特征函数为
(3)期望与方差的线性性质
期望的线性性:对任意常数
方差的性质:对任意常数
随机信号的功率谱
(1)随机信号通过线性系统的功率谱关系
公式:若输入随机信号的功率谱密度为
物理意义:线性系统对输入信号的功率谱进行 “滤波”—— 仅允许与系统频响匹配的频率分量通过,且功率按
(2)平均功率与功率谱密度的关系
公式:随机信号的平均功率等于其功率谱密度在全频域的积分:
推导逻辑:功率谱密度是 “单位频率的功率”,对频率积分相当于 “累加所有频率点的功率”,最终得到总平均功率。
(3)白噪声的功率谱特性
定义:白噪声是一种理想随机信号,其功率谱密度在全频域(
白噪声的功率谱密度
工程意义:实际噪声(如热噪声)在一定带宽内可近似为白噪声,简化分析。
(4)低通滤波器的频响特性
幅频特性:如习题第1章-第3章中第9题中,滤波器在通带
频谱调制
1. 调制带宽的本质
调制的作用是将基带信号(调制信号)的频谱搬移到载波频率附近,带宽由频谱搬移后的边带宽度决定。设调制信号为
2. 各调制方式的带宽公式
AM 调制: AM 信号表达式:
DSB 调制: DSB 信号表达式:
SSB 调制: SSB 信号通过滤波或相移法抑制一个边带,仅保留上边带(
关键区别:边带数量
AM、DSB 保留两个边带,带宽由两个边带的总宽度决定(
SSB 仅保留一个边带,带宽等于单个边带的宽度(
希尔伯特变换
(1)希尔伯特变换的定义
希尔伯特变换是一种线性变换,对信号
(2)正弦信号的希尔伯特变换特性
对于单频正弦信号
若
若
希尔伯特变换对正弦信号实现精确的
(3)解析信号与希尔伯特变换的关系
希尔伯特变换常用来构造解析信号
调频(FM)
1. 调频(FM)的基本原理
FM 是角度调制的一种,瞬时频率随调制信号线性变化,表达式为:
为得到调制信号
2. 关键参数定义与公式
瞬时角频率:
最大角频偏:
调频指数:定义为最大相位偏移或最大频率偏移与调制信号频率之比,
A律13折线编码
1. A 律 13 折线编码的原理
A 律 13 折线是脉冲编码调制(PCM)中常用的非均匀量化方法,通过分段线性化近似对数压缩特性,将输入信号的动态范围划分为多个段落,对小信号采用细量化、大信号采用粗量化,以改善小信号的量化信噪比。
2. 8 位二进制编码的结构
A 律 13 折线的 8 位编码格式为:1 位符号位 + 3 位段落码 + 4 位段内码,具体说明如下:
| 编码位 | 含义 | 取值范围 |
|---|---|---|
| 第 1 位 | 符号位(表示信号正负) | 0(负)/ 1(正) |
| 第 2-4 位 | 段落码(确定信号所在的段落,共 8 个段落) | 000~111(对应 8 个段落) |
| 第 5-8 位 | 段内码(确定段落内的量化电平,每个段落分为 16 个量化级) | 0000~1111(对应 16 个等级) |
段落划分逻辑: 对正半轴信号,按对数规律划分为 7 个段落(负半轴对称),加上原点附近的第 1 段(段 0 和 1 斜率相同合并,正负半轴小信号段合并为 1 条直线,共 13 条折线)。段落码 3 位可表示
以最小量化间隔 Δ=1为单位,正半轴段落参数:
段落号 起始点 结束点 步长 段内间隔数 段落码 0 0 16 1 16 000 1 16 32 1 16 001 2 32 64 2 16 010 3 64 128 4 16 011 4 128 256 8 16 100 5 256 512 16 16 101 6 512 1024 32 16 110 7 1024 2048 64 16 111 段内量化: 每个段落等分为 16 个量化级,4 位段内码可表示
译码电平:取量化间隔中点,需要结合极性。
量化误差:∣输入值−译码电平∣。最大误差小于步长一半(因取中点)。
3. 8 位编码的数学意义
总量化电平数:
编码与量化间隔的关系:
段落码决定量化间隔的倍数(大段落对应大间隔,小段落对应小间隔);
段内码在段落内均匀划分量化级,例如第 1 段(小信号区)的量化间隔最小,第 8 段(大信号区)的间隔最大,实现非均匀量化。
4. 与均匀量化的对比
均匀量化:若量化电平数为 256,需 8 位编码,但所有区间量化间隔相同;
A 律 13 折线:8 位编码结合非均匀分段,用更少的位数实现对小信号的精细量化,等效提升小信号的量化信噪比。
横向滤波器
1. 横向滤波器(Transversal Filter)
定义:一种由抽头延迟线、乘法器和加法器组成的线性滤波器,通过加权求和处理输入信号,常用于信号均衡、信道补偿等场景。
结构特点:包含
2. 均衡器的基本原理
目的:补偿信道失真,减少码间串扰(ISI),使输出信号更接近原始信号。
工作机制:通过调整滤波器系数,对输入信号的不同延迟分量进行加权,抵消信道引起的波形展宽。
3. 卷积与滤波器输出的关系
横向滤波器的输出本质是输入信号与滤波器系数的离散卷积,即:
4. 码间串扰(ISI)与均衡的意义
码间串扰:由于信道带宽限制,当前码元的波形会扩散到相邻码元周期,导致抽样点信号叠加干扰。
均衡作用:通过滤波器设计,使目标抽样点的信号能量最大化,非目标点的干扰最小化。
迫零均衡器
1. 码间串扰 (ISI)
码间串扰是指数字通信系统中,当前码元的波形受到前后码元波形干扰的现象。它由信道的频率选择性衰落或多径传播引起,会导致接收端判决错误。
2. 均衡器与迫零准则
均衡器:用于补偿信道失真、减小码间串扰的信号处理装置
迫零均衡器:通过在特定采样点使码间串扰严格为零的均衡器设计方法,使得整体脉冲响应在指定采样时刻(除主采样点外)为零,从而消除 ISI。
数学模型:设信道冲激响应为
迫零条件:通常设置
3. 峰值失真 (Peak Distortion)
未均衡时:
均衡后:
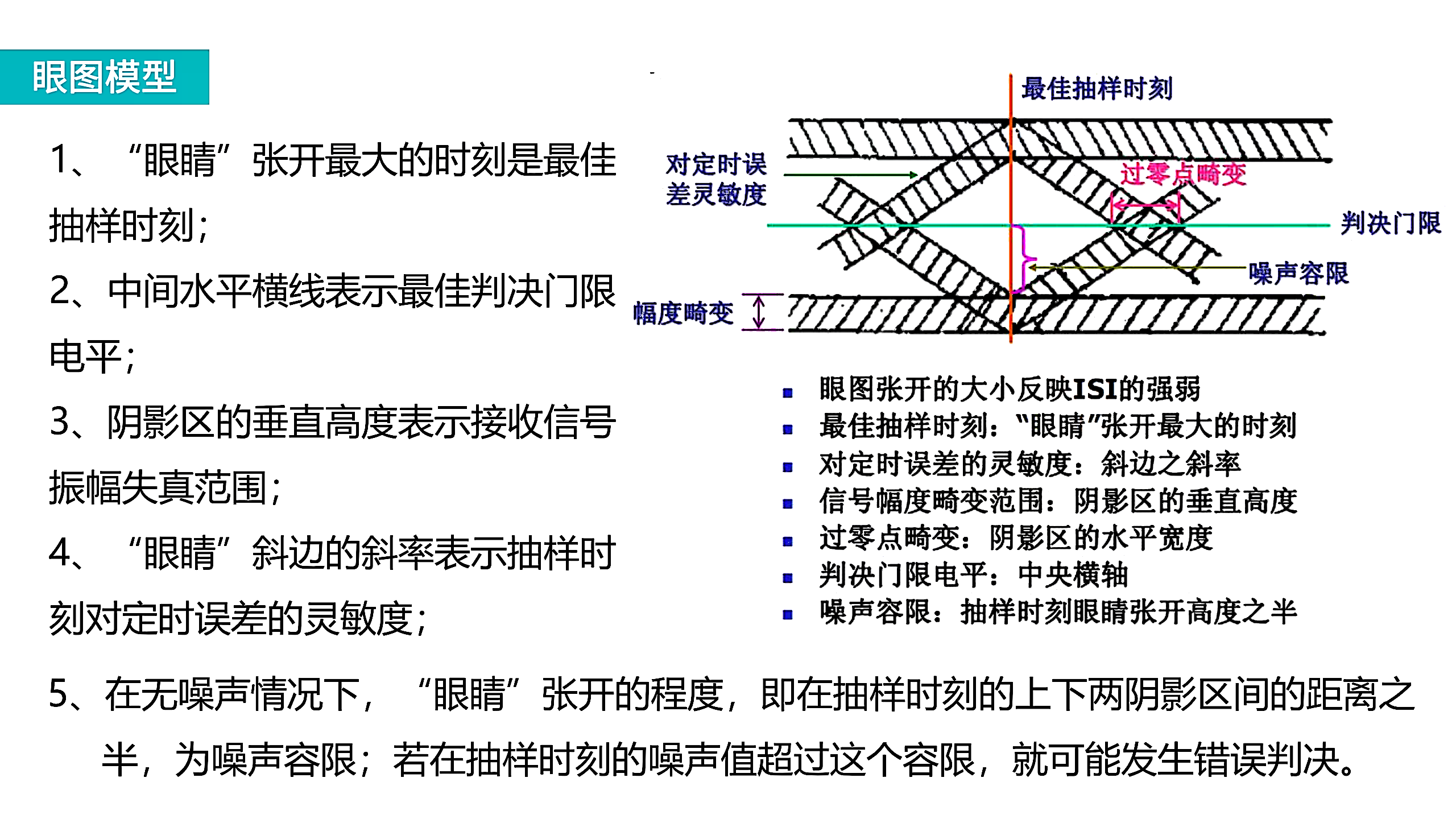
眼图
利用示波器的余辉效应,评价接收信号质量的方法。
AMI/HDB3编码
AMI 码(交替反转码)
1. 编码规则
空号(0):直接映射为 0 电平;
传号(1):交替映射为 + 1 和 - 1 电平,即相邻 “1” 的极性相反。
例:二进制序列 1 0 1 1 0 0 1
→ AMI 码:+1 0 -1 +1 0 0 -1
2. 特点与优势
直流平衡:由于 “1” 的极性交替,信号平均功率为零,消除了直流分量,适合变压器耦合传输;
简单易实现:编码规则直观,硬件实现成本低;
错误检测:若极性交替规律被破坏(如连续两个同极性 “1”),可直接检测传输错误。
3. 局限性
长连 0 问题:当二进制序列中出现长串 “0” 时,AMI 码波形长时间无跳变,导致接收端难以提取时钟同步信号(时钟恢复困难)。
HDB3 码(高密度双极性 3 码)
1. 设计目的
解决 AMI 码中长连 0 导致的同步困难,同时保持直流平衡特性。
2. 编码规则
基本规则:继承 AMI 码的极性交替原则(相邻 “1” 极性相反),但当出现 4 个连续 “0” 时,用特定 “取代节” 替换,避免长连 0。
取代节类型:
若当前非 0 码(“1”)的极性为 “+”,则记为 “+1”,反之记为 “-1”;
设最近一个非 0 码的极性为
B00V:当取代前非 0 码的极性累积数(“+” 和 “-” 的数量差)为偶数时使用;
000V:当累积数为奇数时使用;
V 码(破坏码):极性与前一个非 0 码 相同(打破 AMI 的交替规则),和前面相邻的V极性相反,用于标识取代节,同时确保整个序列的极性交替在宏观上成立。
B 码(平衡码):极性符合 AMI 的交替规则,用于调整极性累积数,使整体直流平衡。
3. 编码示例
二进制序列:1 0 0 0 0 1 0 0 0 0 0 0 1 步骤:
识别 4 个连续 “0” 的位置:第 2-5 位、第 7-10 位(后 4 位 “0” 实际为 6 个连续 “0”,需拆分为两组 4 个 “0”);
第一个 4 连 0:最近非 0 码为 “+1”(第 1 位),极性累积数为 1(奇数),用 “000V” 取代,V 码极性与前非 0 码相同(+1),得:
+1 0 0 0 +V;第二个 4 连 0:前一个非 0 码为 “-1”(第 6 位,按 AMI 规则交替),极性累积数为 0(偶数),用 “B00V” 取代,B 码极性按 AMI 规则应为 “+1”,V 码极性与前非 0 码相同(-1),得:
-1 +B 0 0 -V;最终 HDB3 码:
+1 0 0 0 +V -1 +B 0 0 -V 0 +1(注:实际编码中需严格遵循极性交替和累积数平衡)。
4. 特点与优势
无长连 0:最长连 0 数不超过 3,保证时钟同步信号的提取;
直流平衡:通过 V 码和 B 码的极性调整,整体信号仍无直流分量;
错误检测:V 码破坏极性交替规则,可用于检测传输错误;
兼容性:与 AMI 码兼容,解码端可轻松还原为 AMI 码或原始二进制序列。
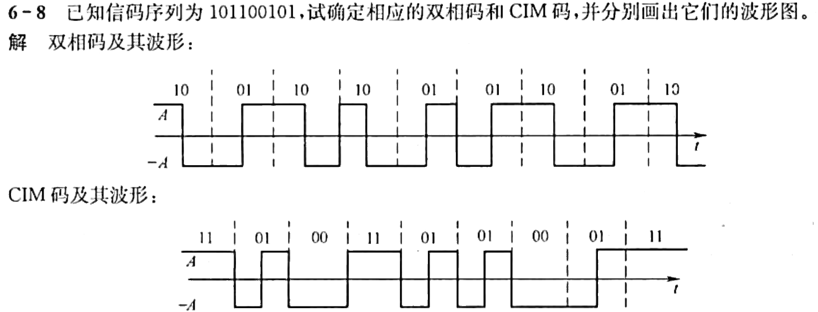
其他编码(双相码、CIM码)
双相码通常指曼彻斯特编码,它将每个二进制码元分成两个相等的间隔。“0” 码用 “01” 表示,即在位中间从低电平跳变到高电平;“1” 码用 “10” 表示,在位中间从高电平跳变到低电平。
CMI码:“1” 用 11、00 交替表示,“0” 用 01 表示。
数字调制
几种不同的数字调制方式
1. 2ASK(二进制振幅键控)
定义:通过改变载波信号的振幅来表示二进制数字信号 “0” 和 “1”。
原理:
当传输 “1” 时,发送载波信号(振幅为 A);
当传输 “0” 时,不发送载波信号(振幅为 0)。
示例:类似 “开关” 控制,如光通信中的开关键控(OOK)。
2. 2PSK(二进制相移键控)
定义:通过改变载波信号的相位来表示二进制信息。
原理:
通常用 0° 相位表示 “1”,180° 相位表示 “0”(或反之)。
特点:相位差为 180°,属于绝对相移调制。
3. 2FSK(二进制频移键控)
定义:通过改变载波信号的频率来表示二进制数据。
原理:
用频率 f1 表示 “1”,频率 f2 表示 “0”,两个频率间隔 Δf 需满足正交条件。
示例:早期 Modem(拨号上网)中常用此方式。
4. 2DPSK(二进制差分相移键控)
定义:基于 2PSK 的改进,通过前后码元的相位差来表示信息,属于相对相移调制。
原理:
不直接使用绝对相位,而是用当前码元与前一码元的相位差(如 0° 表示 “0”,180° 表示 “1”)。
目的:解决 2PSK 的 “相位模糊” 问题(接收端可能误判绝对相位基准)。
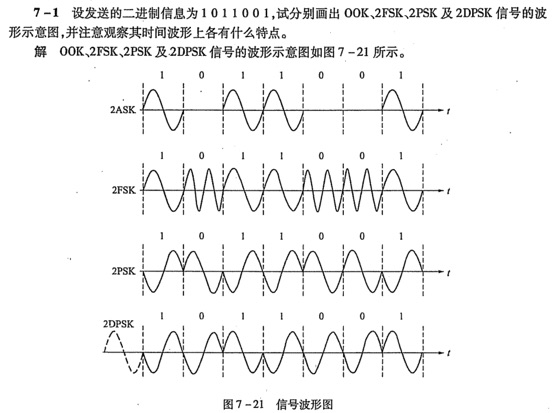
2PSK ——1、0变换时,交界处变载频相位。
2DPSK——0不变,1变,遇到1,变换载频相位。
2ASK——只有1有载频。
2FSK——1低载频,2高载频。
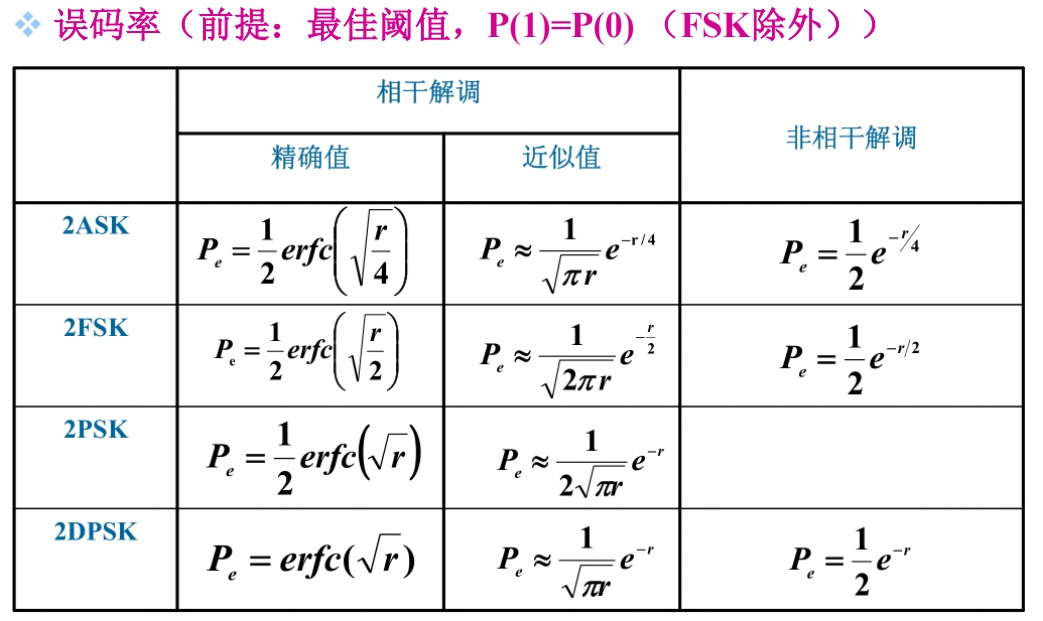
核心技术指标对比
| 指标 | 2ASK | 2PSK | 2FSK | 2DPSK |
|---|---|---|---|---|
| 调制参数 | 振幅 | 相位 | 频率 | 相位差 |
| 抗噪声性能 | 较差(振幅易受噪声影响) | 最佳(相位信息更稳定) | 中等(频率区分需足够间隔) | 接近 2PSK(略低) |
| 带宽需求 | 理论带宽 = 2× 码元速率 | 理论带宽 = 2× 码元速率 | 理论带宽 =Δf+2× 码元速率 | 同 2PSK |
| 频谱效率 | 高(带宽利用率高) | 高 | 低(需额外频率间隔) | 高 |
| 实现复杂度 | 简单(硬件要求低) | 中等(需相位基准) | 中等(需频率合成器) | 中等(需差分编码) |
| 相位模糊问题 | 无 | 有(接收端可能误判 0°/180°) | 无 | 无(差分编码消除基准依赖) |
通信原理习题
第1章-第3章
1.某通信系统在接收端测得接收信号功率为 2W,若已知噪声功率为 2×10⁻³W,则该系统的接收端信噪比
Note
接收端信噪比 r 的计算公式为:
信噪比(SNR) 定义为信号功率与噪声功率的比值,反映信号在噪声环境中的质量。
用分贝(dB)表示时,公式为
2.传输十六进制独立等概信号的码元宽度为 0.5ms,则其传码率
Note
传码率
信息速率
传码率(波特率) 表示单位时间内传输的码元个数,单位为波特(Baud),与码元宽度成反比:
信息速率 表示单位时间内传输的信息量,单位为 bit/s。对于 M 进制等概信号,每个码元的信息量为
3.如果随机过程的
Note
自相关函数是用来描述同一个信号在不同时刻的相似程度的数学工具。
对于信号
当
当
若信号变化慢(如低频信号),不同时刻的波形相似,
若信号变化快(如高频噪声),波形迅速改变,
4.某信号的自相关函数为
Note
根据维纳 - 辛钦定理,功率谱密度
维纳 - 辛钦定理:建立了随机过程时域自相关函数与频域功率谱密度的一一对应关系,是信号频域分析的核心理论之一。
门函数的傅里叶变换:宽度为T的门函数
5.设均值为 0,方差为
Note
窄带过程可表示为:
利用三角函数公式展开
同相分量:
与载波
正交分量:
与载波
平均功率是信号在长时间内的平均能量。数学上,对于平稳过程,它是
计算:由于均值是 0, 方差
6.某信号

Note
信号的平均功率 P 等于其双边功率谱密度
对于此题,两侧三角形总面积即为平均功率:
7.已知某八进制数字通信系统的信息速率为
Note
信息速率
八进制(
传码率
误码率定义为错误码元数与总码元数的比值:
8.设
Note
高斯随机变量 X 的概率密度函数为:
若
均值(期望): 由期望的线性性质
方差: 由方差的性质
因 Y 服从正态分布
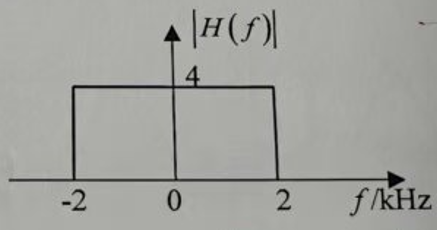
9.设白噪声的双边功率谱密度为
Note
根据随机信号通过线性系统的功率谱密度关系:
当
当
根据
平均功率等于输出功率谱密度在全频域的积分:
由于
代入
第5章
1.对最高频率为
A.
B.
C.
D.
Note
AM 调制: AM 信号频谱包含载波分量、上边带(调制信号正频率分量搬移)和下边带(调制信号负频率分量搬移)。调制信号最高频率为
DSB 调制: DSB 信号抑制了载波,仅保留上边带和下边带,带宽由两个边带决定,同样为
SSB 调制: SSB 信号仅保留一个边带(上边带或下边带),因此带宽等于调制信号最高频率
2.对下述载波电话多路复用系统框图的描述,不正确的是( B )。

A、发送端各调制器的载频设置必须遵循保护频带原则。
B、发送端低通滤波器的作用是滤除带外噪声。
C、该框图只适用于模拟信号的多路传输,不适用于数字信号的多路传输。
D、接收端的各路带通滤波器用来过滤每路SSB信号,因此中心频率各不相同。
Note
发送端各调制器载频
发送端低通滤波器(LPF)的作用是限制消息信号的最高频率(限制信号带宽,如语音信号限带至 3.4kHz),而非 “滤除带外噪声”(噪声抑制更多由信道或后续滤波处理)。
接收端带通滤波器(BPF)中心频率对应各路载频
3.将信号
Note
希尔伯特变换(Hilbert Transform,HT)对正弦信号的作用是相位滞后
对于信号
4.设基带信号带宽为 5kHz,对其进行上边带调制,载频为 20kHz。则接收端带通滤波器的中心频率为
Note
上边带调制(SSB)后,信号频谱搬移到载波频率
上边带调制(SSB)的信号带宽等于基带信号带宽
信道噪声为加性白噪声,其双边功率谱密度
代入
5.求 FM 信号
Note
最大角频偏(
给定信号:
瞬时相位
瞬时角频率
计算导数:
角频偏
故最大角频偏为:
调频指数定义为最大相位偏移或最大频率偏移与调制信号频率之比。
最大相位偏移法:相位偏移
在 FM 中, 调频指数
或者:
代入得:
6.已知均值为零的基带信号
xxxxxxxxxx151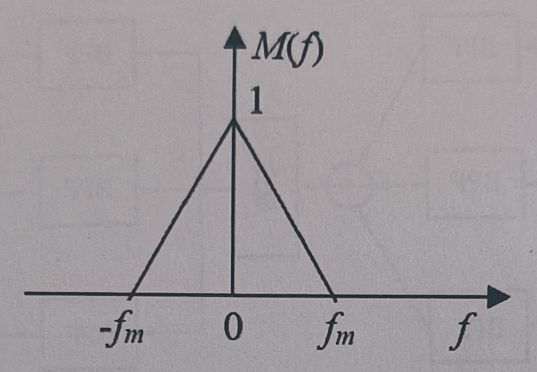2> [!NOTE]4>5> 对于基带信号 $m(t)$,DSB 信号的频谱为:$S_{\text{DSB}}(f) = \frac{1}{2} M(f - f_c) + \frac{1}{2} M(f + f_c)$6>7> - SSB 通过滤波从 DSB 信号中提取一个边带:8> - 下边带 (LSB):保留 $M(f + f_c)$ (负频率部分) 和 $M(f - f_c)$ 的镜像 (正频率部分)。9> - 频谱表达式:10>11> LSB 频谱是 DSB 频谱的一半(因另一半边带被滤除):12>13> $ S_{LSB}(f) = \begin{cases} \frac{1}{2} M(f + f_c) & \text{for } f \in [−f_c, −f_c + f_m] \\ \frac{1}{2} M(f - f_c) & \text{for } f \in [f_c - f_m, f_c] \\ 0 & \text{elsewhere} \end{cases} $14>15> 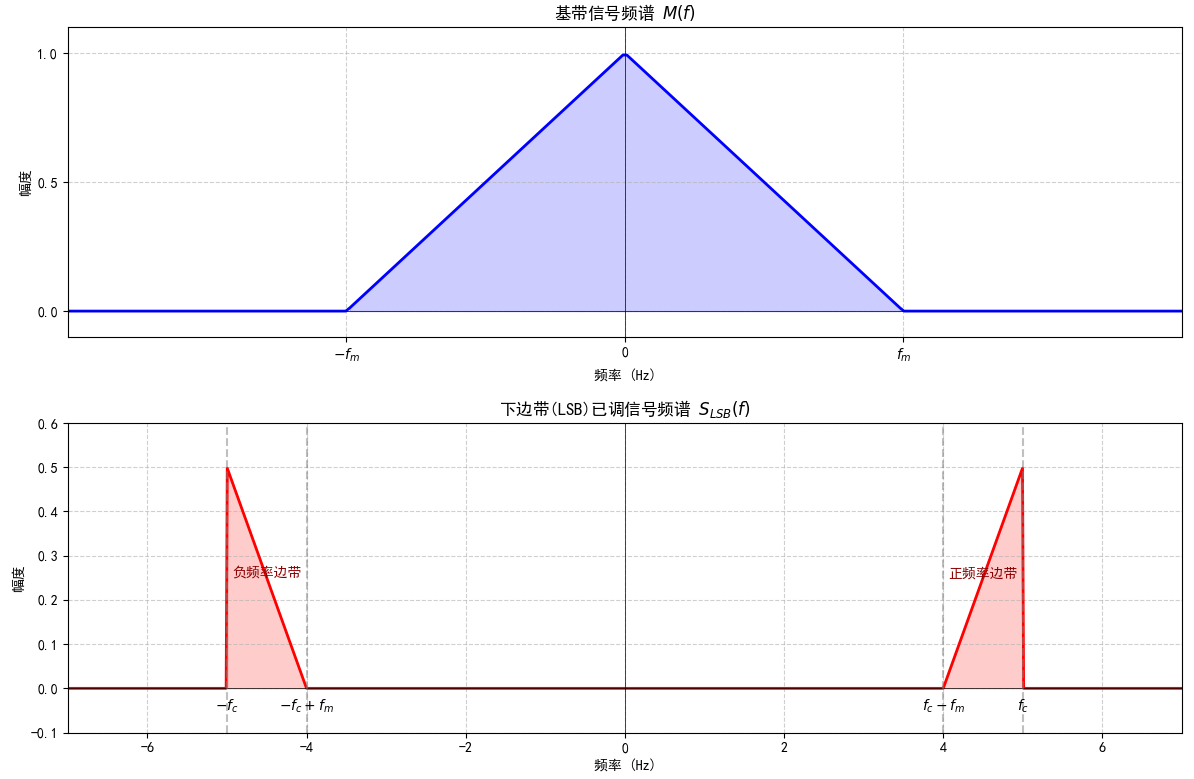
第10章
1.设低频模拟信号的频率范围为0~20kHz,则可以无失真恢复信号的最小采样频率为
Note
对于带宽为
2.模拟信号
Note
均匀量化是将模拟信号的取值范围 等间隔划分,每个间隔对应一个量化电平。设模拟信号的取值范围为
将
3.均匀量化的量化间隔
A、
Note
均匀量化的量化误差(量化噪声)的最大值为
4.与均匀量化相比,非均匀量化( D )。
A. 降低了系统复杂度。 B. 主要改善了大信号的量化信噪比。 C. 扩大了达到某种信噪比要求的信号动态范围。 D. 改善了小信号的量化信噪比。
Note
均匀量化:量化间隔
5.量化会产生量化噪声,衡量量化噪声对系统通信质量影响的指标是( D )。
A. 量化噪声功率 B. 量化信号功率 C. 量化间隔大小 D. 量化信噪比
Note
量化间隔
量化信噪比(Signal-to-Quantization Noise Ratio, SQNR)定义为信号功率与量化噪声功率的比值,直接反映了噪声对信号质量的影响程度(比值越高,噪声影响越小)。
6.采用A律13折线对信号进行非均匀量化编码,通常编码输出是用( C )位二进制数表示。
A. 6 B. 7 C. 8 D. 9
Note
A 律 13 折线的 8 位编码格式为:1 位符号位 + 3 位段落码 + 4 位段内码
7.采用 A 率 13 折线编码,设最小量化间隔为 1 个单位,已知抽样脉冲值为 -158 单位:
(1) 试求此时编码器输出码组,并计算量化误差(译码电平取量化间隔的中点); (2) 写出对应于该 7 位码(不包括极性码)的均匀量化 11 位码(采用自然二进制码)。
Note
极性码:抽样值为负,故极性码为
0。段落确定:幅度为 158 单位。幅度 158 满足 128 ≤ 158 < 256,故位于段落 4。
段落码:段落 4 对应二进制码
段内码:段落 4 的起始点为 128 ,步长为 8 。量化间隔下界公式:
解得
输出码组:完整 8 位码组为极性码 + 段落码 + 段内码
译码电平:译码电平取量化间隔中点,公式为:
代入段落起始点 128、
抽样值为负,故译码电平为 -156 单位。
量化误差:量化误差定义为输入值与译码电平之差的绝对值:
均匀量化 11 位自然二进制码:
对于该7位码 0 1 0 0 0 0 1 1,152为该7位码起点,156为该7位码中点。
这里取起点152进行二进制转换(11 位, 高位补零)
输出:均匀量化 11 位码为
8.【课本 例题10-2】
Note
编码过程如下:
(1) 确定极性码
(2) 确定段落码
由于
由于
经过以上三次比较,编出的段落码
(3) 段内码
第四次比较结果为
第五次比较结果为
第六次比较结果为
第七次比较结果为
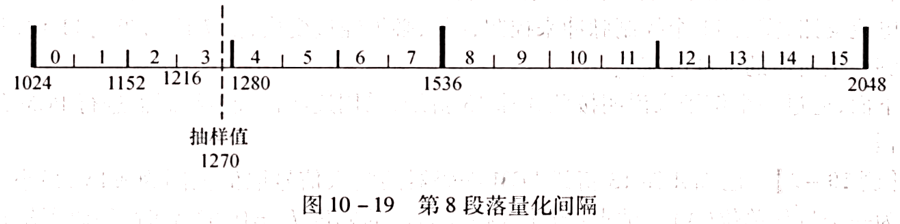 经过以上编码过程, 对于模拟抽样值
经过以上编码过程, 对于模拟抽样值
第6章
1.设有一个三抽头的横向滤波器,其
Note
横向滤波器的输出公式为:
每个系数
已知三抽头系数:
计算各抽样点输出
当
当
当
同理计算
结果汇总
| 抽样点 k | 输出 |
|---|---|
| 0 | |
| 0 | |
| 其他 | 0 |
2.设计 3 个抽头的迫零均衡器, 以减小码间串扰。已知,
Note
设 3 个抽头的均衡器系数为
均衡器输出
均衡器抽头系数:
均衡前峰值失真:根据公式:
计算求和项:
代入公式:
均衡后峰值失真:
3.【课本 习题6-3】设二进制随机序列由
Note
证明 由上式可得
令
将上式代入《通信原理 (第 7 版) 》教材式 (6.1-14), 可知离散谱消失, 即
证毕。
4.【课本 习题6-7】已知信码序列为 1011000000000101 , 试确定相应的 AMI 码及
Note
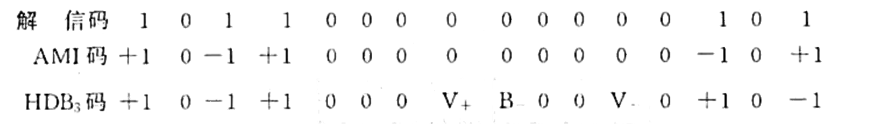
其波形均为三电平
5.【课本 习题6-11】设基带传输系统的发送滤波器、信道及接收滤波器组成的总特性为
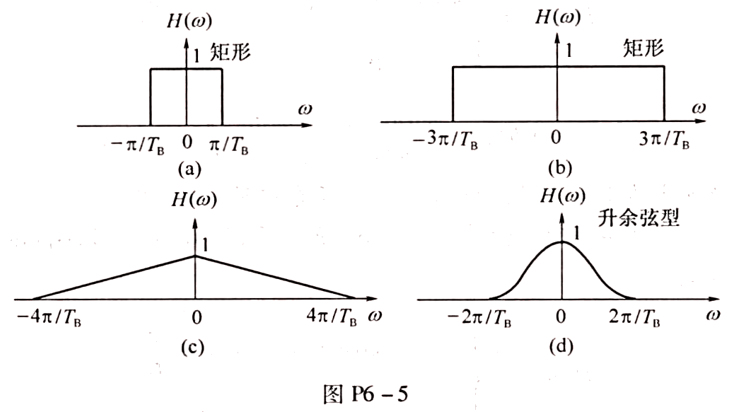
Note
方法 1: 根据奈奎斯特准则, 当传码率
因此, 当
容易验证: 除 (c) 之外, (a)、(b) 和 (d) 均不满足上式所述的无码间串扰条件。
方法 2: 由
则以实际速率
(a)
(b)
(c)
(d)
6.【课本 习题6-17、18】某二进制数字基带系统所传送的是单极性基带信号, 且数字信息“1”和“0”的出现概率相等。
(1) 若数字信息为“1”时, 接收滤波器输出信号在抽样判决时刻的值
(2) 若要求误码率
若将上题中的单极性信号改为双极性信号, 而其他条件不变, 重做上题中的各问,并进行比较。
Note
解(1)已知
(2)若要求
若将上题中的单极性信号改为双极性信号,而其他条件不变,重做上题中的各问,并进行比较。
解 (1) 双极性基带系统的误码率
(2)若要求
评注:在
7.【课本 习题6-24】设计一个三抽头迫零均衡器。已知输入信号
(1) 求三个抽头的最佳系数;
(2) 比较均衡前后的峰值失真。
Note
解(1)由本辅导书中式 (6.1-49) 可知,确定抽头系数
据此,可列出三个抽头系数
将样值
解得
(2) 由式
其余
输入峰值失真为
输出峰值失真为
均衡后的峰值失真减小 8.87 倍。
第7章
1.设发送的二进制信息为
(1) 当载波频率为
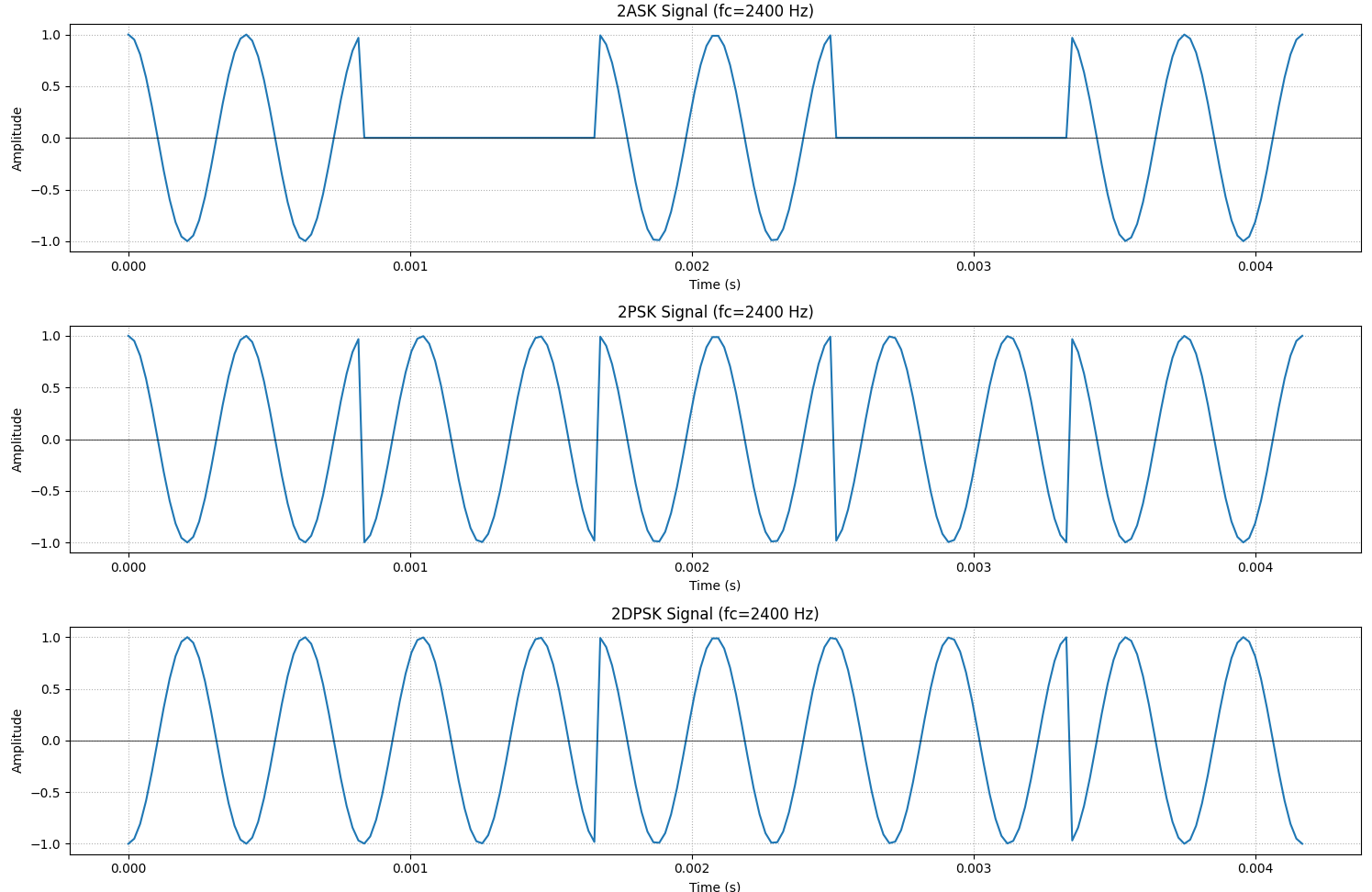
(2) 2FSK的两个载波频率分别为 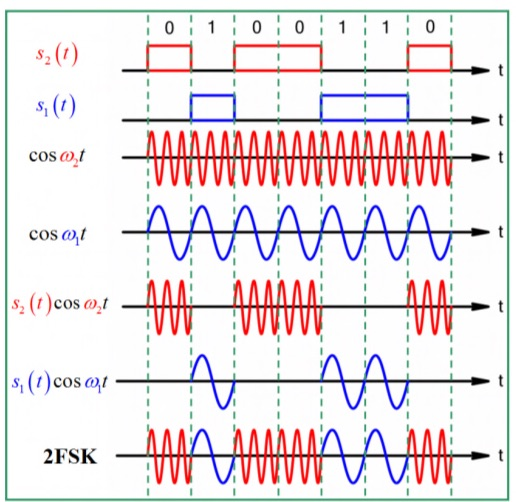
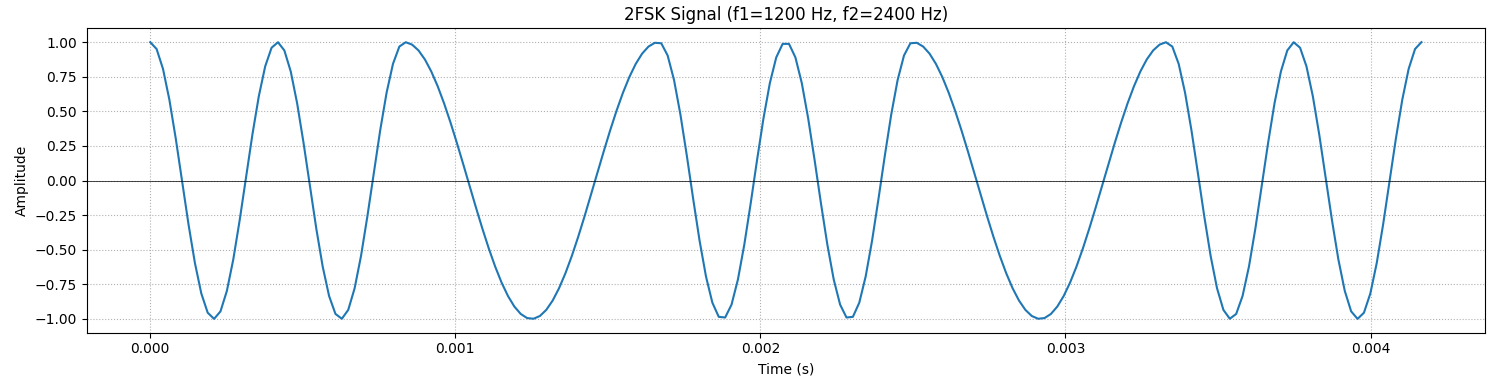
(3) 上述各已调信号的带宽是多少?
Note
2ASK / 2PSK / 2DPSK 带宽:
理论公式:
2FSK 带宽:
理论公式:
2.设某2FSK传输系统的码元速率为
(1) 试画出一种2FSK信号调制器原理框图,并画出2FSK信号的时间波形;
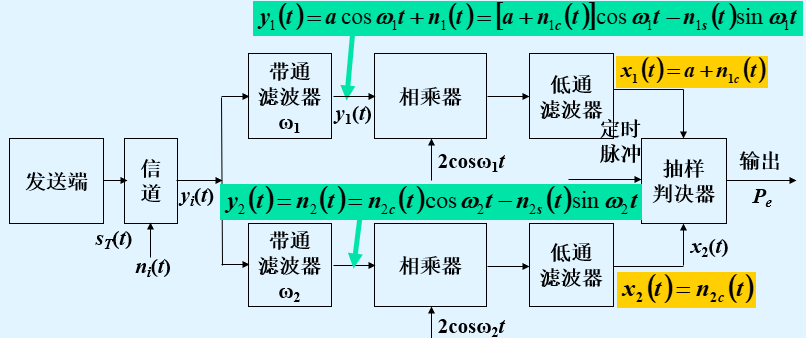
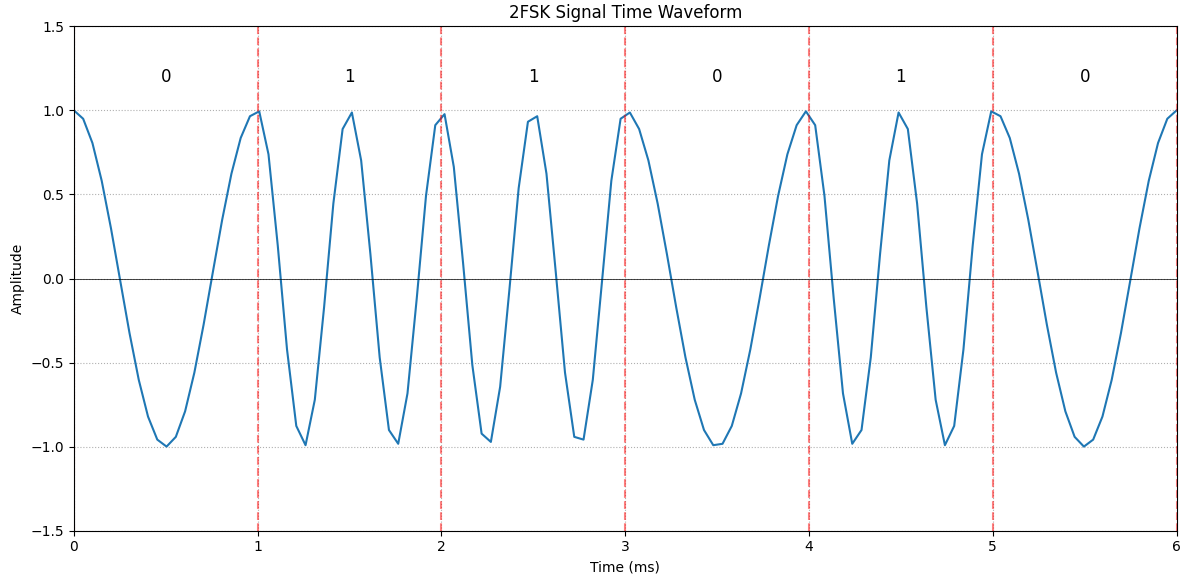
(2) 试画出2FSK信号的功率谱密度示意图。
xxxxxxxxxx711. 连续谱: 2 - 以f1=1000Hz为中心,主瓣范围约0~2000Hz(带宽2Rb=2000Hz),呈sinc²衰减; 3 - 以f2=2000Hz为中心,主瓣范围约1000~3000Hz,与前者重叠1000~2000Hz; 4 - 旁瓣按1/f²衰减,幅度随频率升高快速下降。 5
62. 离散谱: 7 - 在f1和f2处存在冲击函数,幅度为连续谱峰值的1/4(理论值)。 3.采用
(1) 2FSK信号的带宽;
(2) 同步检测法解调时系统的误码率。
Note
2FSK(二进制频移键控)信号的带宽主要由两个载波频率的间隔和码元速率决定。其带宽计算公式为:
已知
分贝与线性值的转换基于对数运算,公式为:
已知输入信噪比为
计算得到近似值为4.
在 2FSK 系统中,每个带通滤波器需匹配单个载波频率的信号带宽。对于矩形脉冲调制的信号,其带宽约为:
带通滤波器输出端的信噪比
将
4.假设采用2DPSK方式在微波线路上传送二进制数字信息。已知码元速率
(1)采用相干解调一码反变换时,接收机输入端所需的信号功率。
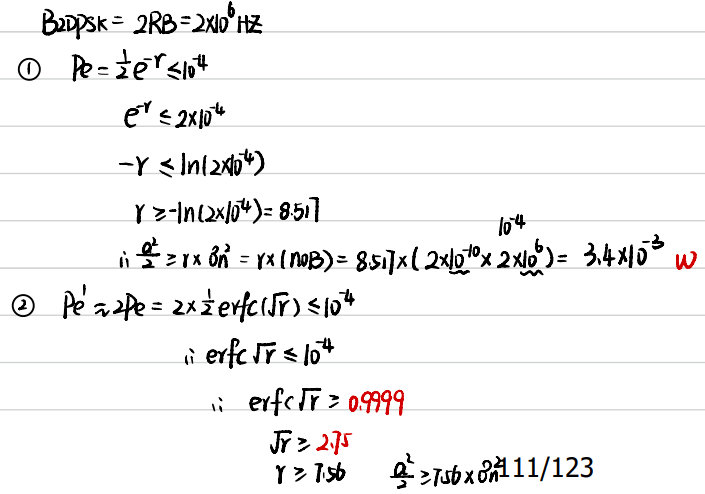
第11章
1.码组11010,其码长和码重为多少?
Note
其码长n=5,码重W=3。
码长:指一个码组中包含的码元(bit)数量,即码组的长度。
码重:指码组中 “1” 的个数,反映码组的非零元素数量。
2.已知一个
试列出其所有许用码组,并求出其监督矩阵。
Note
(1)
(2)

 解题过程:
解题过程:
码长
信息位 u 共有
许用码组
以
计算
计算
计算
计算
计算
计算
计算
最终编码结果:
对于系统形式的生成矩阵
信息位部分I为一个
校验位部分P是一个
接下来计算P的转置矩阵
最后,把
3.已知一个(7, 4)循环码的全部码组为
试写出该循环码的生成多项式
Note
(1) 生成多项式
(2) 生成矩阵
或写成
通过分析码组,最小权重的非零码字对应的多项式为
0001011 对应多项式
构造生成矩阵
生成矩阵
对应的矩阵形式为:
将 G 化为典型阵:
典型生成矩阵形式为
4.【课本 习题11-6】已知某线性码的监督矩阵为
试列出其所有可能的码组。
Note
